ある信頼性エンジニアが、冷蔵庫コンプレッサーの不良が原因の保証請求を予測したいと考えています。エンジニアは、前年の月ごとの故障データを収集および分析します。
エンジニアは今後の製造スケジュールが毎月配送される1000ユニットであることを把握しています。故障データはワイブル分布を使用してモデル化できます。処理前の保証データの形式を変更した後、エンジニアは保証予測を使用して将来の保証請求を予測します。
- サンプルデータを開く、コンプレッサー故障前処理.MWX.
- を選択します。
- 開始時間に、開始時を入力します。
- 終了時間に、終了時を入力します。
- 度数 (オプション)に、度数を入力します。
- 予測をクリックします。各時間間隔の生産量に、「1000」と入力します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
現在の保証請求の要約の表での結果では、データ収集期間内に稼働している12,000台のコンプレッサーのうち、69台が故障すると示されています。ワイブル分布で得られた推定値に基づいて、期間内に約69台のコンプレッサーが故障すると予測されました。
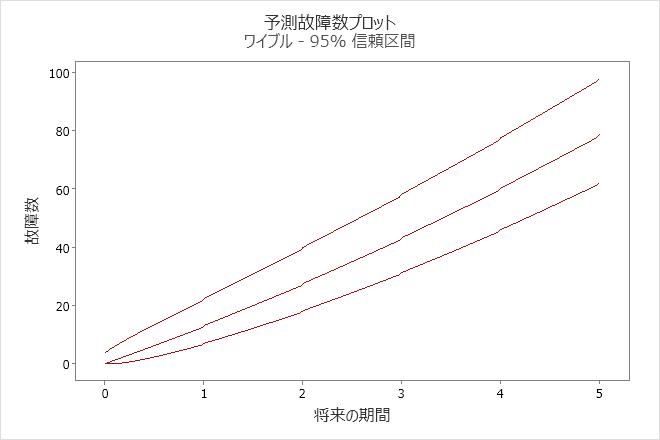
予測故障数の表と予測故障数プロットを使用して、エンジニアは95%の信頼度をもって、今後5か月間にコンプレッサーの予測追加故障台数がおよそ62~98台の区間に収まることを結論づけることができます。
度数の度数を使用します
分布パラメータ
| 分布 | 形状 | 尺度 |
|---|---|---|
| ワイブル | 1.26494 | 398.062 |
現在の保証請求の要約
| 合計個数 | 12000 |
|---|---|
| 観測された故障数 | 69 |
| 期待される故障数 | 68.5201 |
| 95%ポアソン信頼区間 | (53.2630, 86.7876) |
| 将来故障するリスクがある個数 | 11931 |
生産スケジュール
| 将来の期間 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 生産数量 | 1000 | 1000 | 1000 | 1000 | 1000 |
予測故障数の表
| 95%ポアソン信頼区間 | ||||
|---|---|---|---|---|
| 将来の期間 | 潜在的な故障数 | 予測故障数 | 下限 | 上限 |
| 1 | 12931 | 13.1073 | 7.0000 | 22.3660 |
| 2 | 13931 | 27.4930 | 18.1933 | 39.8678 |
| 3 | 14931 | 43.1798 | 31.2722 | 58.1271 |
| 4 | 15931 | 60.1892 | 45.9516 | 77.4449 |
| 5 | 16931 | 78.5416 | 62.1373 | 97.9488 |