エンジニアは、再設計されたジェットエンジンのコンプレッサーケースの信頼性を評価したいと思っています。設計をテストするために、各コンプレッサーケースに飛翔体を1体投げ込みます。飛翔体を衝突させた後、コンプレッサーを12時間おきにチェックして故障の有無を確認します。
ここでは、生命データでの回帰分析を使ってケースの設計、飛翔体の重量、故障時間の関係を評価します。また、1%と5%のエンジン故障が予想される故障時間も推定します。データのモデル化には、ワイブル分布を使用します。
- サンプルデータを開く、ジェットエンジン信頼性.MWX.
- を選択します。
- 応答は打ち切られていない/任意打ち切りデータを選択します。
- 変数/開始変数に、開始を入力します。
- 終了変数に、終了を入力します。
- モデルに、計画と重みを入力します。
- 因子 (オプション)に、計画を入力します。
- 推定をクリックします。新しい予測変数を入力するに、新設計新重量を入力します。
- 次のパーセントに対する百分位数を推定するに1 5と入力し、OKをクリックします。
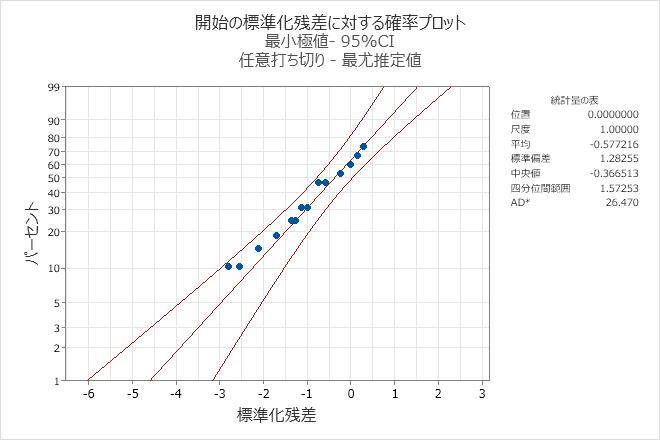
- グラフをクリックします。標準化残差に対する確率プロットを選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
回帰表では、デザインと重量のp値が0.05のα水準で有意です。したがって、エンジニアは、ケースデザインと飛翔体の重量にはともに故障時間において統計的に有意な影響があると結論づけます。予測変数の係数は、ケースデザイン、飛翔体の重量、およびエンジンの故障時間の間にある関係を記述する式の定義に使用できます。
百分位数表には、ケースデザインと飛翔体の重量の各組み合わせにおける第1百分位数と第5百分位数が示されます。1%~5%のエンジンが故障するまでの経過時間は、すべての飛翔体の重量において標準的なケースデザインより新しいケースデザインのほうが長くなります。たとえば、10ポンドの飛翔体を使用した後、1%の標準的なケースデザインのエンジンが約101.663時間後に故障すると予測できます。新しいケースデザインでは、1%のエンジンが約205.882時間後に故障すると予測できます。
標準化残差の確率プロットでは、点がほぼ直線に従います。したがって、エンジニアはモデルが適切であると仮定できます。
応答変数の開始:開始 終了: 終了
打ち切り
| 打ち切り情報 | 計数 |
|---|---|
| 右打ち切り値 | 25 |
| 区間打ち切り値 | 23 |
推定法:最尤法
分布: ワイブル
加速変数との関係: 線形
回帰表
| 95.0%正規信頼区間 | ||||||
|---|---|---|---|---|---|---|
| 予測変数 | 係数 | 標準誤差 | z値 | p値 | 下限 | 上限 |
| 切片 | 6.68731 | 0.193766 | 34.51 | 0.000 | 6.30754 | 7.06709 |
| 計画 | ||||||
| 標準 | -0.705643 | 0.0725597 | -9.72 | 0.000 | -0.847857 | -0.563428 |
| 重み | -0.0565899 | 0.0212396 | -2.66 | 0.008 | -0.0982187 | -0.0149611 |
| 形状 | 5.79286 | 1.07980 | 4.02001 | 8.34755 | ||
対数尤度 = -88.282
Anderson-Darling (調整済み) 適合度
標準化残差 = 26.470
パーセンタイル表
| 95.0%正規信頼区間 | ||||||
|---|---|---|---|---|---|---|
| パーセント | 計画 | 重み | パーセンタイル | 標準誤差 | 下限 | 上限 |
| 1 | 標準 | 5.0 | 134.911 | 17.6574 | 104.385 | 174.363 |
| 1 | 標準 | 7.5 | 117.113 | 16.0279 | 89.5591 | 153.144 |
| 1 | 標準 | 10.0 | 101.663 | 16.3830 | 74.1295 | 139.423 |
| 1 | 新規 | 5.0 | 273.214 | 36.8022 | 209.819 | 355.763 |
| 1 | 新規 | 7.5 | 237.171 | 32.6878 | 181.028 | 310.726 |
| 1 | 新規 | 10.0 | 205.882 | 32.8675 | 150.568 | 281.518 |
| 5 | 標準 | 5.0 | 178.749 | 16.9676 | 148.404 | 215.300 |
| 5 | 標準 | 7.5 | 155.168 | 14.1107 | 129.836 | 185.443 |
| 5 | 標準 | 10.0 | 134.698 | 15.4568 | 107.568 | 168.670 |
| 5 | 新規 | 5.0 | 361.994 | 36.0778 | 297.761 | 440.084 |
| 5 | 新規 | 7.5 | 314.239 | 28.8741 | 262.450 | 376.247 |
| 5 | 新規 | 10.0 | 272.783 | 30.6102 | 218.928 | 339.887 |