特定のパーセントの百分位数の推定点
p番目の パーセンタイル ポイント xpは、応答 pに必要なストレス水準です。
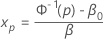
xpの推定値を求めるには、次の式を使用します。
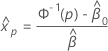
ここで、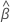
および
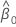は、の最尤推定値です。 
および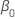
.
プロビット分析の対数位置分布は、対数正規分布、対数ロジスティック分布、ワイブル分布です。対数位置分布の場合、前の式では対数スケールの百分位数が推定されます。これらの分布を使用してデータのスケールで百分位数を推定するには、次の式を使用します。
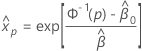
特定のパーセントの百分位数の標準誤差
パーセンタイルの標準誤差の計算には、デルタ法を使用します。推定されたパーセンタイルの標準誤差には、次の式があります。
ここで、分散は 
次の形式があります。
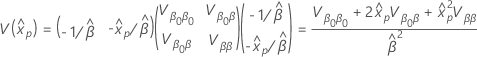
そして、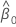 
および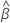
次の形式があります。
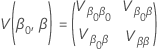
プロビット分析の対数位置分布は、対数正規分布、対数ロジスティック分布、ワイブル分布です。対数ロケーション分布の場合、前の式では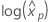 
.分散と分散共分散行列の定義 
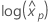従う。
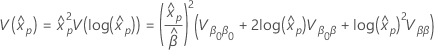
特定のパーセントの百分位数の基準信頼区間
両面、100(1 - 
) を 
です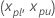 
を次の式で求めます。
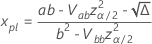
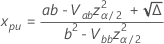
ここで、
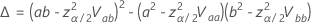
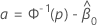
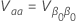
プロビット分析の対数位置分布は、対数正規分布、対数ロジスティック分布、ワイブル分布です。対数ロケーション分布の場合、前の式では対数スケールの間隔が推定されます。データのスケールで区間を推定するには、前の式の信頼限界を指数化します。
特定のストレス値における故障確率または生存確率の基準信頼区間
両面、100(1 - 
) 故障確率、 
です 
.生存確率については、 
、間隔は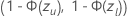 
.次の式は計算を示しています。
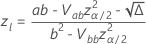
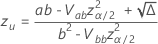
ここで、
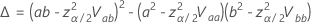
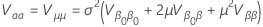
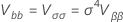
および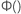
は、分析の分布の累積分布関数です。
プロビット分析の対数位置分布は、対数正規分布、対数ロジスティック分布、ワイブル分布です。ログ・ロケーション分布の場合は、次の定義を置き換えます。
参考文献
フィデューシャル信頼区間の導出には、フィラーの定理を使用します。フィラーの定理は、次の参考文献にあります。
Finney, D. J. (1971). Probit analysis, (Third edition), London: Cambridge University Press.
プロビットモデルとパーセンタイルの推定の詳細については、次のリファレンスを参照してください。
Cox, D. R. and Snell, E. J. (1989). The analysis of binary data (Second edition), London: Chapman & Hall.
