ある航空機用フロントガラスのエンジニアは、フロントガラスが飛翔体による衝撃にどの程度耐えられるかを一定の速度範囲について調査したいと考えています。エンジニアは、フロントガラスのランダムサンプルに8つの速度のいずれかで飛翔体を当て、フロントガラスが衝撃に耐えたかどうかを記録します。
エンジニアは、飛翔体による衝撃を受けたときに特定の割合のフロントガラスが割れる速度範囲を調べるために、プロビット分析を実行します。
- サンプルデータを開く、 フロントガラスのストレス.MWX.
- を選択します。
- 事象/試行フォーマットでの応答を選択します。
- 事象数に、破損を入力します。
- 試行回数に、Nを入力します。
- ストレス (刺激)に、ストレスを入力します。
- 仮定する分布から、正規を選択します。
- OKをクリックします。
結果を解釈する
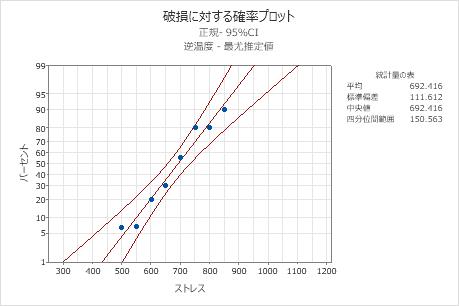
分布の適合を評価するために、エンジニアは0.1の有意水準を使用します。適合度p値(0.977および0.975)が有意水準より大きくなると、確率プロットの点がほぼ直線上に収まります。このため、エンジニアは正規分布モデルがデータにうまくあてはまることを仮定できます。
有意な効果を評価するために、エンジニアは0.05の有意水準を使用します。ストレスのp値(0.000)が有意水準(0.05)より低いため、エンジニアは飛翔体の速度が風防ガラス破損の有無に統計的に有意な効果を及ぼしていると結論づけます。
百分位数の表には、95%の信頼度で、風防ガラスの1%は300.019~501.649 mph(マイル/時)の速度範囲で破損することが示されます。
分布: 正規
応答情報
| 変数 | 値 | 計数 |
|---|---|---|
| 破損 | 事象 | 37 |
| 非事象 | 52 | |
| N | 合計 | 89 |
推定法:最尤法
回帰表
| 変数 | 係数 | 標準誤差 | z値 | p値 |
|---|---|---|---|---|
| 定数 | -6.20376 | 1.06565 | -5.82 | 0.000 |
| ストレス | 0.0089596 | 0.0015615 | 5.74 | 0.000 |
| 自然 | ||||
| 応答 | 0 |
対数尤度 = -38.516
適合度検定
| 方法 | カイ二乗 | 自由度 | p値 |
|---|---|---|---|
| ピアソン | 1.19972 | 6 | 0.977 |
| 逸脱 (deviance) | 1.22858 | 6 | 0.975 |
パラメータ推定値
| 95.0%正規信頼区間 | ||||
|---|---|---|---|---|
| パラメータ | 推定 | 標準誤差 | 下限 | 上限 |
| 平均 | 692.416 | 18.3649 | 656.421 | 728.410 |
| 標準偏差 | 111.612 | 19.4518 | 79.3167 | 157.058 |
パーセンタイル表
| 95.0%フィデューシャル信頼区間 | ||||
|---|---|---|---|---|
| パーセント | パーセンタイル | 標準誤差 | 下限 | 上限 |
| 1 | 432.767 | 45.8542 | 300.019 | 501.649 |
| 2 | 463.192 | 41.0355 | 345.266 | 525.291 |
| 3 | 482.496 | 38.0450 | 373.838 | 540.427 |
| 4 | 497.018 | 35.8391 | 395.242 | 551.902 |
| 5 | 508.830 | 34.0781 | 412.585 | 561.304 |
| 6 | 518.884 | 32.6067 | 427.289 | 569.364 |
| 7 | 527.699 | 31.3403 | 440.133 | 576.480 |
| 8 | 535.592 | 30.2277 | 451.589 | 582.896 |
| 9 | 542.771 | 29.2352 | 461.967 | 588.771 |
| 10 | 549.379 | 28.3398 | 471.482 | 594.217 |
| 20 | 598.480 | 22.4304 | 540.595 | 636.280 |
| 30 | 633.886 | 19.4337 | 587.639 | 669.400 |
| 40 | 664.139 | 18.1881 | 624.815 | 700.723 |
| 50 | 692.416 | 18.3649 | 656.409 | 733.152 |
| 60 | 720.692 | 19.8068 | 685.039 | 768.545 |
| 70 | 750.945 | 22.4716 | 713.104 | 808.979 |
| 80 | 786.351 | 26.5977 | 743.723 | 858.524 |
| 90 | 835.453 | 33.3805 | 783.926 | 929.497 |
| 91 | 842.060 | 34.3538 | 789.210 | 939.174 |
| 92 | 849.239 | 35.4233 | 794.925 | 949.712 |
| 93 | 857.132 | 36.6126 | 801.183 | 961.326 |
| 94 | 865.948 | 37.9558 | 808.140 | 974.328 |
| 95 | 876.002 | 39.5048 | 816.041 | 989.192 |
| 96 | 887.814 | 41.3455 | 825.280 | 1006.70 |
| 97 | 902.335 | 43.6350 | 836.585 | 1028.27 |
| 98 | 921.639 | 46.7171 | 851.535 | 1057.03 |
| 99 | 952.065 | 51.6465 | 874.954 | 1102.50 |