斉次ポアソン工程
斉次ポアソン工程(HPP)は、定数強度関数λを持つポアソン工程です。故障間区間は、独立しており、同じ分布で、平均 = 1/λで指数分布に従うランダム変数です。
斉次ポアソン工程の強度変数は定数であるため、このモデルは故障間区間が体系的に増減しない場合のみ適切です。斉次ポアソン工程は、改良したり劣化したりするシステムには適切ではありません。
べき法則工程
次の強度関数を持つ非斉次ポアソン工程。
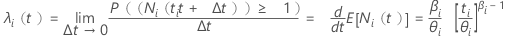
強度関数は、故障率や修復率を表します。形状の値(β)は、システムが向上しているか、劣化しているか、または一定であるかによって異なります。
- 0 < β < 1の場合、故障/修復率は減少しています。つまり、システムは向上しています。
- β = 1の場合、故障/修復率は一定です。つまり、システムは安定しています。
- β > 1の場合、故障/修復率は増加しています。つまり、システムは劣化しています。
注
デフォルトの推定法(最尤法)では、べき法則工程はAMSAAモデルまたはCrow-AMSAAモデルとも呼ばれます。(元のCrow-AMSAAモデルでは、尺度パラメータは、λ = 1/θ^(β)です)。1つのシステムだけが考慮され、最小二乗推定法が使用される場合、べき法則工程はDuaneモデルと呼ばれます。
表記
| 用語 | 説明 |
|---|---|
| βi | 形状 |
| θi | 尺度 |
| Ni | 区間(0,t] でのi番目のシステムの故障数 |
