このトピックの内容
生存確率
信頼性関数R(t)は、生存関数S(t)としても知られており、時間tを超えてユニットが正常に機能する確率を示します。
計算式
R(t) = 1 - F(t)
システムを正常に機能させるためにはすべての成分が正常に機能する必要があるため、一連のシステムの信頼性は、成分の信頼性関数による結果です。個別成分から成る一連のシステムにおける信頼性を計算するには、すべての成分の信頼性関数を掛け合わせます。
表記
| 用語 | 説明 |
|---|---|
| F(t) | 選択した分布のCDF |
生存確率に対する信頼限界
生存確率に対する信頼限界の上限と下限は、次の計算式で定義されます。
計算式
ここで、 と
と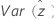 (生存確率の分散)は、分布に基づいて次のように定義されます。
(生存確率の分散)は、分布に基づいて次のように定義されます。
最小極値、正規、対数正規、ロジスティック、対数ロジスティック

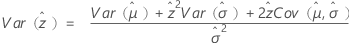
3-パラメータ対数正規、3-パラメータ対数ロジスティック
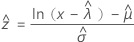
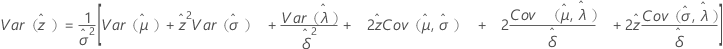
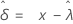
ワイブル
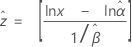
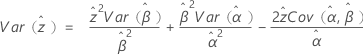
3-パラメータワイブル
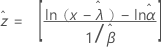
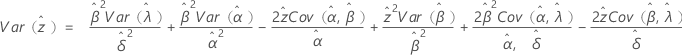
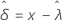
指数
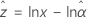

2-パラメータ指数

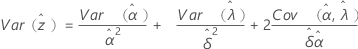
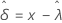
表記
| 用語 | 説明 |
|---|---|
| zα | 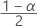 の標準正規分布の上限棄却値(100α%が信頼水準の場合)。 の標準正規分布の上限棄却値(100α%が信頼水準の場合)。 |




