パラメトリック分布分析（右打ち切り）の例

ある信頼性エンジニアは、タービンアセンブリ用のエンジン巻揚部品の故障率を調査して、エンジン巻揚部品が故障するまでの時間を特定しようとしています。温度が高い場合、巻揚部品の分解が早くなりすぎる可能性があります。

エンジニアは80°Cおよび100°Cの故障回数を記録します。ただし、いくつかのユニットは故障する前に検定から取り除く必要があります。したがって、このデータは右打ち切りです。パラメトリック分布分析（右打ち切り）を使用して以下を判断します。

さまざまな故障率に達するまでの時間。エンジニアは特に百分位数0.1に関心があります。
70時間正常に動作し続ける巻揚部品の割合
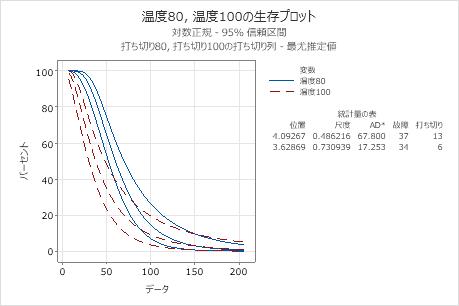
エンジン巻揚部品の生存関数（生存プロットに表示される）
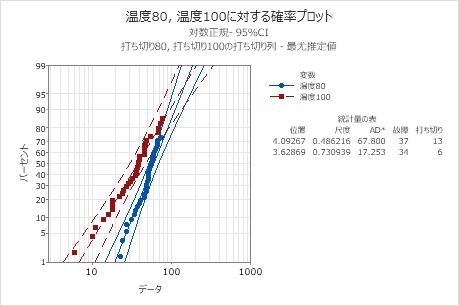
データの対数正規分布への適合（確率プロットに表示される）

サンプルデータを開く、エンジン巻揚部品の信頼性.MTW.
統計 > 信頼性/生存時間 > 分布分析（右打ち切り） > パラメトリック分布分析を選択します。
変数に、温度80温度100を入力します。
仮定する分布から、対数正規を選択します。
打ち切りをクリックします。打ち切り列を使用するで打ち切り80打ち切り100を入力します。
打ち切りの値に、「0」と入力します。OKをクリックします。
推定をクリックします。次の追加パーセントに対する百分位数を推定するに「0.1」と入力します。
次の時間 (値) に対する確率を推定するに、「70」と入力します。OKをクリックします。
グラフをクリックします。生存プロットを選択します。
各ダイアログボックスでOKをクリックします。

結果を解釈する

百分位数表を使用すると、さまざまな割合での巻揚部品の故障時間を判断できます。80℃では、1%の巻揚部品が19.3281時間までに故障します。0.1番目の百分位数の値は、エンジニアが分析で要求するもので、表にも示されます。80℃では、0.1%の巻揚部品が13.3317時間までに故障します。100℃では、0.1%の巻揚部品が3.93505時間までに故障します。したがって、温度が上がると、約9.5時間まで百分位数は低下します。

生存確率表を使用して、エンジニアは70時間以上正常に機能すると予測される巻揚部品の割合を判断できます。80°Cでは、37.43%の巻揚部品が70時間以上正常に機能すると予測されます。100°Cでは、19.82%の巻揚部品が70時間以上正常に機能すると予測されます。

エンジニアは、生存プロットを使用して時間の経過に伴う生存確率を確認でき、確率プロットを使用して対数正規分布がデータに適合することを確認できます。

80° C

変数: 温度80

打ち切り

打ち切り情報	計数
打ち切られていない値	37
右打ち切り値	13

推定法:最尤法

分布: 対数正規

パラメータ推定値

			95.0%正規信頼区間
パラメータ	推定	標準誤差	下限	上限
位置	4.09267	0.0719681	3.95161	4.23372
尺度	0.486216	0.0606247	0.380799	0.620816

対数尤度 = -181.625

適合度

Anderson-Darling (調整済み)
67.800

分布の特性

			95.0%正規信頼区間
	推定	標準誤差	下限	上限
平均 (MTTF)	67.4153	5.55245	57.3656	79.2255
標準偏差	34.8145	6.79827	23.7435	51.0476
中央値	59.8995	4.31085	52.0192	68.9735
第1四分位数 (Q1)	43.1516	3.29526	37.1531	50.1186
第3四分位数 (Q3)	83.1475	7.37690	69.8763	98.9392
四分位間範囲 (IQR)	39.9959	6.33317	29.3245	54.5505

パーセンタイル表

			95.0%正規信頼区間
パーセント	パーセンタイル	標準誤差	下限	上限
0.1	13.3317	2.51559	9.21026	19.2975
1	19.3281	2.83750	14.4953	25.7722
2	22.0674	2.92559	17.0178	28.6154
3	24.0034	2.97261	18.8304	30.5975
4	25.5709	3.00355	20.3126	32.1906
5	26.9212	3.02621	21.5978	33.5566
6	28.1265	3.04403	22.7506	34.7727
7	29.2276	3.05881	23.8074	35.8819
8	30.2501	3.07165	24.7910	36.9113
9	31.2110	3.08326	25.7170	37.8788
10	32.1225	3.09409	26.5962	38.7970
20	39.7837	3.20997	33.9646	46.5999
30	46.4184	3.41015	40.1936	53.6073
40	52.9573	3.75669	46.0833	60.8568
50	59.8995	4.31085	52.0192	68.9735
60	67.7517	5.15910	58.3584	78.6569
70	77.2958	6.45920	65.6184	91.0514
80	90.1863	8.58211	74.8412	108.678
90	111.696	12.8103	89.2100	139.849
91	114.958	13.5112	91.3052	144.738
92	118.610	14.3120	93.6288	150.255
93	122.759	15.2417	96.2426	156.581
94	127.565	16.3437	99.2372	163.979
95	133.276	17.6863	102.753	172.866
96	140.314	19.3873	107.026	183.955
97	149.477	21.6739	112.500	198.608
98	162.590	25.0764	120.175	219.977
99	185.634	31.3868	133.271	258.570

生存確率表

		95.0%正規信頼区間
時間	確率	下限	上限
70	0.374299	0.263102	0.497141

100° C

変数: 温度100