このトピックの内容
確率プロット
確率プロットを使用すると、選択した分布のデータに対する適合度を評価できます。点が適合線に緊密に従っている場合、その分布はデータに十分適合していると仮定できます。
- プロット上の点は、ノンパラメトリック法に基づく推定百分位数で、分布に依存しません。ポインターをデータ点上に置くと、観測された故障時間と推定累積確率が表示されます。
- 適合線(中心線)は適合分布に基づいています。ポインターを適合線上に置くと、各種パーセントの百分位数表が表示されます。
- 左側の直線は、各百分位数の信頼区間の下限をつないだものです。右側の直線は、各百分位数の信頼区間の上限をつないだものです。
出力例
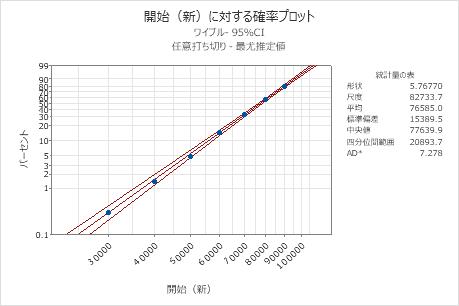
解釈
新型マフラーに関するデータの場合、点が適合線に従っているように見えます。したがって、ワイブル分布がこのデータの適切な選択肢と仮定できます。この適合線は、形状 = 5.76770、尺度 = 82733.7のワイブル分布に基づいています。
生存プロット
生存プロットでは、品目が特定時間まで正常に機能する確率が図示されます。このため、生存プロットでは、時間の経過に伴う製品の信頼性が示されます。
- 中心線は、時間の経過に伴う推定された信頼性です。
- 右側の線は、各時点の信頼性の上限をつないだものです。左側の線は、各時点の信頼性の下限をつないだものです。
ポインターを生存曲線上に置くと、時間と生存確率の表が表示されます。
分布がデータにあてはまる場合にのみ、このプロットを使用してください。分布がデータにあてはまらなければ、これらの推定値は不正確になります。分布がデータにあてはまるかどうかを判断するには、分布識別プロット、確率プロット、および適合度の測度を使用します。
出力例
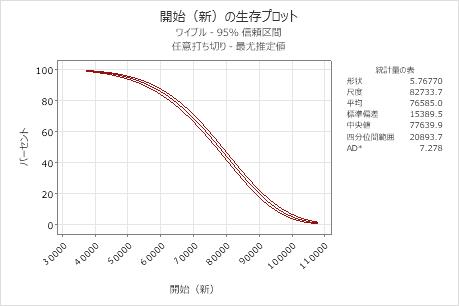
解釈
新型マフラーのデータでは、新型マフラーが50,000マイルまで正常に機能する確率は約95%です。この生存関数は、形状 = 5.76770で、尺度 = 82733.7のワイブル分布に基づいています。
累積故障プロット
製品の信頼性を製品の故障時期で記述するために、累積故障プロットでは、品目が特定時間tまでに故障する累積パーセントを表示します。累積故障関数は、1 - 生存関数を表します。
- 中心線は、時間の経過に伴う推定された累積故障パーセントです。
- 右側の線は、各時点の累積故障パーセントの下限をつないだものです。左側の線は、各時点の累積故障パーセントの上限をつないだものです。
ポインターを曲線上に置くと、累積故障確率と故障時間が表示されます。
分布がデータにあてはまる場合にのみ、このプロットを使用してください。分布がデータにあてはまらなければ、これらの推定値は不正確になります。分布がデータにあてはまるかどうかを判断するには、分布識別プロット、確率プロット、および適合度の測度を使用します。
出力例
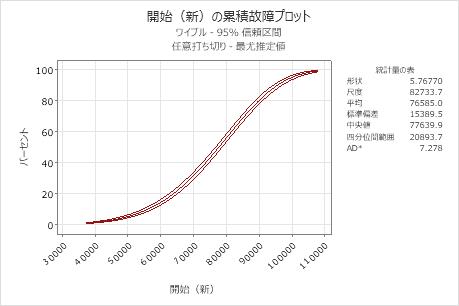
解釈
新型マフラーのデータの場合、新型マフラーが50,000マイルまでに故障する確率は約5%です。この累積故障関数は、形状 = 5.76770で、尺度 = 82733.7のワイブル分布に基づいています。
ハザードプロット
- 減少: 品目が故障する確率は、時間の経過とともに減少します。一般的に、減少するハザードは製品寿命の初期に発生します。
- 一定: 品目は一定の率で故障します。一般的に、一定のハザードは、故障がランダムに発生する場合の製品の耐用年数内に発生します。
- 増加: 品目が故障する確率は、時間の経過とともに増加します。一般的に、増加するハザードは、摩耗の場合のように製品寿命の後期に発生します。
ハザード関数の形状は、データと選択した分布に基づいて決定されます。ポインターをハザード曲線上に置くと、故障時間とハザード率の表が表示されます。
分布がデータにあてはまる場合にのみ、このプロットを使用してください。分布がデータにあてはまらなければ、これらの推定値は不正確になります。分布がデータにあてはまるかどうかを判断するには、分布識別プロット、確率プロット、および適合度の測度を使用します。
出力例
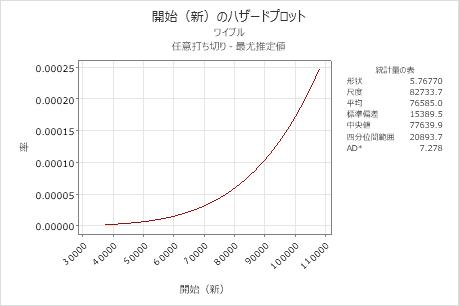
解釈
新型マフラーのデータの場合、ハザード関数は、形状 = 5.76770、尺度 = 82733.7のワイブル分布に基づいています。ここで、ハザード率は時間の経過とともに増加します。つまり、新型マフラーが故障する確率は、時間の経過とともに増加します。
多重故障モードグラフ
多重故障データでは、各故障モードのグラフが表示されます。
- 確率プロットを使用すると、選択した分布のデータに対する適合度を評価できます。点が適合線に緊密に従っている場合、その分布を使用してデータをモデル化します。
- 生存プロットを使用すると、品目が特定時間まで正常に機能する確率を評価できます。このため、生存プロットでは、時間の経過に伴う製品の信頼性が示されます。
- ハザード関数を使用すると、ユニットが存続する時間の関数として故障尤度(特定時間tの短期的な故障率)が得られます。ハザードプロットには、時間の経過に伴う故障率の傾向が示されます。
出力例
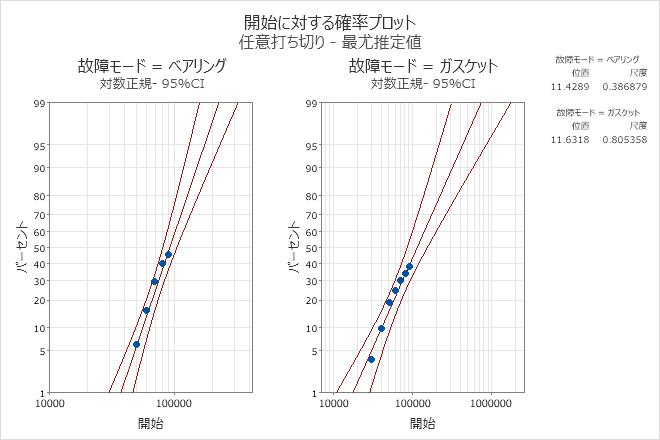
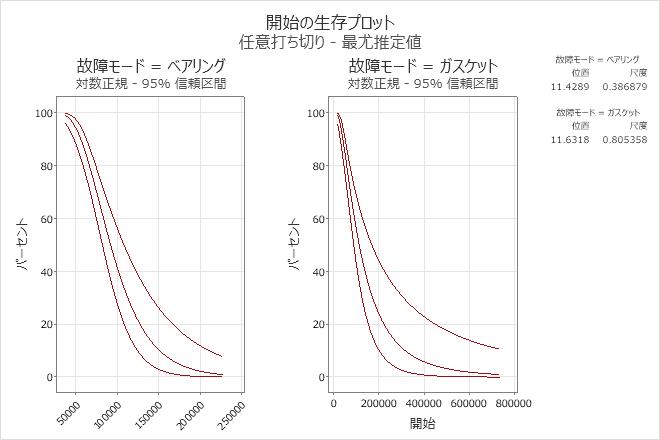
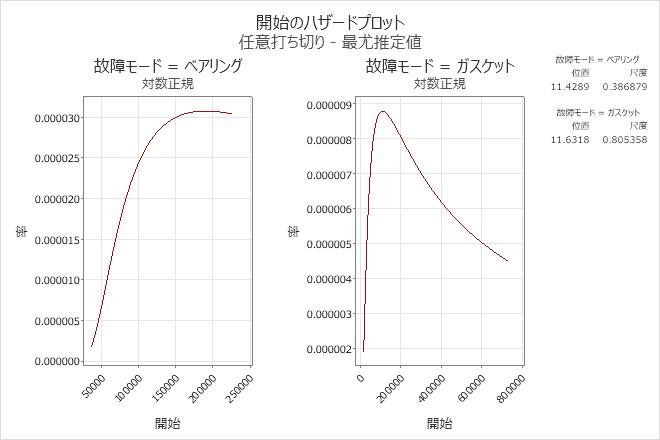
解釈
ポンプデータの場合、対数正規分布は、両方の故障モードをモデル化するのに適切な選択肢と言えます。パラメータは、ベアリング故障の場合、位置 = 11.4289、尺度 = 0.386879であり、ガスケット故障の場合、位置 = 11.6318、尺度 = 0.805358となります。
ポンプがベアリング故障なしで70,000マイルまで正常に機能する確率は約70%であり、ガスケット故障なしで70,000マイルまで正常に機能する確率も約70%です。
各故障モードのハザード率は時間の経過に伴い少しずつ増加しますが、ガスケット故障ではその後減少します。
