パラメトリック分布分析（任意打ち切り）の例

ある信頼性エンジニアが、新しいタイプのマフラーの信頼性を評価し、50,000マイル保証に対して予想される保証請求の比率を推定します。エンジニアは古いタイプのマフラーと新しいタイプのマフラー両方の故障データを収集します。マフラーは、故障がないかどうか10,000マイルごとに点検されました。

エンジニアは10,000マイルごとの故障数を記録します。したがって、このデータは任意打ち切りです。パラメトリック分布分析（任意打ち切り）を使用して以下を判断します。

さまざまなマフラーの故障率に達するまでのマイル数
50,000マイル正常に動作し続けるマフラーの割合
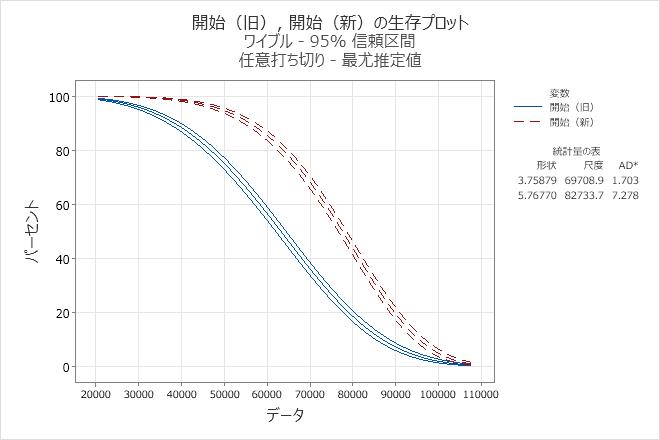
マフラーの生存関数（生存プロットに表示される）
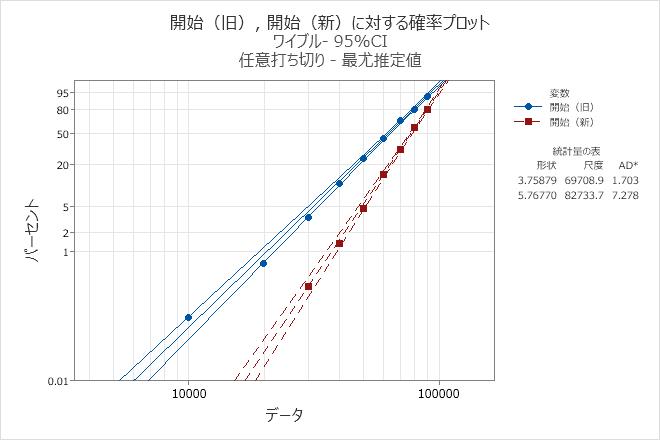
データのワイブル分布への適合（確率プロットに表示される）

サンプルデータを開く、マフラーの信頼性.MTW.
統計 > 信頼性/生存時間 > 分布分析（任意打ち切り） > パラメトリック分布分析を選択します。
開始変数に、開始（旧）開始（新）を入力します。
終了変数に、終了（旧）終了（新）を入力します。
度数列 (オプション)に、度数（旧）度数（新）を入力します。
仮定する分布から、ワイブルを選択します。
推定をクリックします。次の時間 (値) に対する確率を推定するに、「50000」と入力します。OKをクリックします。
グラフをクリックします。生存プロットを選択します。
各ダイアログボックスでOKをクリックします。

結果を解釈する

エンジニアは、百分位数表を使用して、古いマフラーと新しいマフラーがさまざまなパーセントで故障するマイル距離を判断できます。古いマフラーでは、10%のマフラーが38,307マイルまでに故障します。新しいマフラーでは、10%のマフラーが56,006.1マイルまでに故障します。

エンジニアは、生存確率表を使用して、少なくとも50,000マイルまで正常に機能することが予測されるマフラーの比率を判断できます。少なくとも50,000マイルで正常に機能するマフラーの比率を判断することもできます。古いマフラーでは50,000マイル以降の生存確率は約75.07%です。新しいマフラーでは50,000マイル以降の生存確率は約94.67%です。

エンジニアは、生存プロットを使用して、異なるマイル距離での生存確率、およびワイブル分布がデータに適合することを確認する確率プロットを表示します。

古いマフラー

変数の開始:開始（旧）終了: 終了（旧）

度数: 度数（旧）

打ち切り

打ち切り情報	計数
右打ち切り値	83
区間打ち切り値	965
左打ち切り値	1

推定法:最尤法

分布: ワイブル

パラメータ推定値

			95.0%正規信頼区間
パラメータ	推定	標準誤差	下限	上限
形状	3.75879	0.100226	3.56739	3.96045
尺度	69708.9	618.000	68508.1	70930.7

対数尤度 = -2083.927

適合度

Anderson-Darling (調整済み)
1.703

分布の特性

			95.0%正規信頼区間
	推定	標準誤差	下限	上限
平均 (MTTF)	62963.8	585.834	61826.0	64122.5
標準偏差	18685.0	417.812	17883.8	19522.1
中央値	63232.6	618.048	62032.7	64455.6
第1四分位数 (Q1)	50042.1	692.162	48703.7	51417.3
第3四分位数 (Q3)	76037.5	658.037	74758.6	77338.2
四分位間範囲 (IQR)	25995.4	610.478	24826.0	27219.9

パーセンタイル表

			95.0%正規信頼区間
パーセント	パーセンタイル	標準誤差	下限	上限
1	20501.3	730.973	19117.5	21985.2
2	24686.2	762.138	23236.7	26226.0
3	27535.4	773.441	26060.5	29093.8
4	29766.4	777.507	28280.8	31329.9
5	31630.7	778.040	30141.9	33193.0
6	33249.1	776.589	31761.3	34806.5
7	34689.8	773.926	33205.6	36240.3
8	35995.3	770.488	34516.4	37537.6
9	37194.3	766.537	35721.9	38727.5
10	38307.0	762.243	36841.8	39830.5
20	46771.7	714.662	45391.8	48193.6
30	52987.5	671.735	51687.1	54320.5
40	58301.0	638.544	57062.8	59566.1
50	63232.6	618.048	62032.7	64455.6
60	68106.3	614.500	66912.5	69321.4
70	73237.9	634.997	72003.8	74493.1
80	79117.5	693.244	77770.3	80487.9
90	87026.8	827.620	85419.8	88664.1
91	88068.9	849.547	86419.5	89749.8
92	89195.0	874.226	87497.9	90925.0
93	90425.9	902.323	88674.6	92211.8
94	91791.7	934.808	89977.7	93642.3
95	93338.0	973.162	91450.0	95265.0
96	95139.2	1019.83	93161.2	97159.2
97	97330.7	1079.31	95238.2	99469.3
98	100206	1161.47	97954.9	102508
99	104650	1296.79	102139	107223

生存確率表

		95.0%正規信頼区間
時間	確率	下限	上限
50000	0.750682	0.727911	0.771856

新しいマフラー

変数の開始:開始（新）終了: 終了（新）

度数: 度数（新）

* 注 * 8つのケースが使用されました

* 注 * 2ケースに欠損値が含まれていたか、度数がゼロでした。