ある信頼性エンジニアが、地下鉄の車両で使用される2種類のブレーキ部品の故障率を比較したいと考えています。エンジニアは、29両の車両について交換時間と部品タイプに関するデータを収集します。部品は故障するたびに修理して再び使用されました。
エンジニアはノンパラメトリック成長曲線を使用して、分布モデルを仮定せずにデータを評価します。これらのデータでは、離脱したブレーキ部品はありません。したがって、すべてのデータは正確な故障時間を示します。
- サンプルデータを開く、ブレーキの信頼性.MWX.
- を選択します。
- 変数/開始変数に、日数を入力します。
- システム情報で、システムIDを選択して、IDを入力します。
- グループ変数を選択して、タイプを入力します。
- OKをクリックします。
結果を解釈する
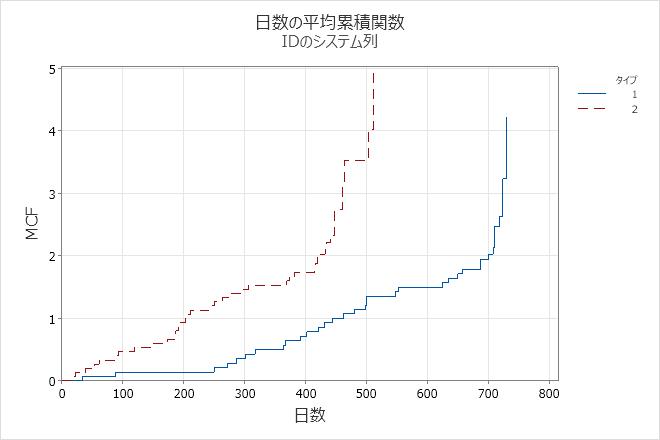
平均累積関数のノンパラメトリック推定値、およびそれに対応する標準誤差と信頼限界がグループごとに表示されます。たとえば、タイプ1のブレーキ部品の場合、650日目の平均累積関数は1.71429です。つまり、650日目の平均累積修理数は、すべてのシステムで平均化した場合、約1.7になります。エンジニアは、95%の信頼性をもって、650日目でのタイプ1部品の真の平均累積関数が、1.27912~2.29750に収まると判断できます。
エンジニアは、平均累積差関数を使用して、グループ間の比較を行います。たとえば、500日目のタイプ2ブレーキ部品は、タイプ1ブレーキ部品より平均で2.16420多く故障しました。エンジニアは、95%の信頼性をもって、500日目での真の平均累積差(タイプ1 - タイプ2)が、−3.23488~−1.09352に収まると判断できます。
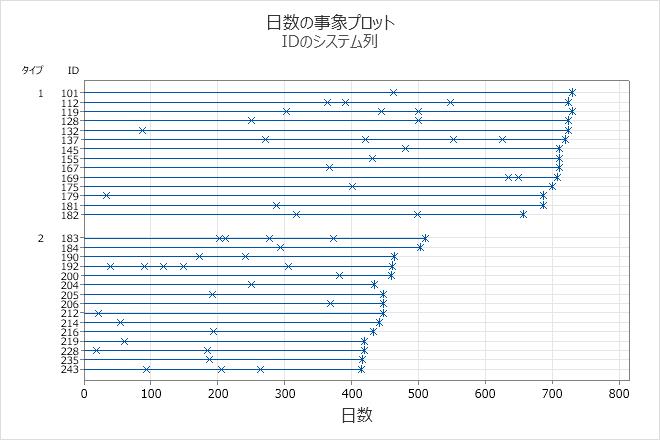
事象プロットは、各システムで故障が発生した時間を示します。個々の直線は、観測最終日まで延びています。このプロットは、グループ内およびグループ間での傾向を示します。このプロットでは、通常システム故障が一定の割合で発生するものとします。200日目で、タイプ2ブレーキ部品は、タイプ1ブレーキ部品より非常に多く故障します。
- タイプ2ブレーキ部品を表す関数は、約450日目まで比較的に直線で、曲線ではありません。したがって、タイプ2ブレーキ部品の故障率は450日目まで比較的一定です。
- タイプ1ブレーキ部品を表す関数は、およそ200日目から700日目にかけて直線で、そこから急増します。したがって、タイプ1ブレーキ部品の故障率は700日目までほぼ一定ですが、その後急増します。
- タイプ1ブレーキ部品を表す関数は、タイプ2ブレーキ部品の関数の右側です。したがって、タイプ2ブレーキ部品に比べタイプ1ブレーキ部品のほうが故障数は少ないことになります。
- タイプ 1
- システム: IDノンパラメトリック推定値
平均累積関数表
95%正規信頼区間 時間 平均累積関数 標準誤差 下限 上限 システム 33 0.07143 0.068830 0.01081 0.47218 179 88 0.14286 0.093522 0.03960 0.51540 132 250 0.21429 0.109664 0.07859 0.58426 128 272 0.28571 0.120736 0.12481 0.65408 137 287 0.35714 0.128060 0.17686 0.72120 181 302 0.42857 0.132260 0.23407 0.78471 119 317 0.50000 0.133631 0.29613 0.84423 182 364 0.57143 0.132260 0.36303 0.89945 112 367 0.64286 0.128060 0.43506 0.94990 167 391 0.71429 0.157421 0.46374 1.10019 112 402 0.78571 0.149098 0.54168 1.13970 175 421 0.85714 0.170747 0.58008 1.26653 137 431 0.92857 0.158574 0.66444 1.29771 155 444 1.00000 0.174964 0.70969 1.40906 119 462 1.07143 0.158574 0.80165 1.43200 101 481 1.14286 0.137661 0.90253 1.44718 145 498 1.21429 0.149098 0.95456 1.54468 182 500 1.28571 0.187044 0.96675 1.70992 119 500 1.35714 0.191853 1.02872 1.79042 128 548 1.42857 0.219328 1.05735 1.93013 112 552 1.50000 0.242226 1.09304 2.05848 137 625 1.57143 0.280566 1.10744 2.22982 137 635 1.64286 0.259653 1.20522 2.23940 169 650 1.71429 0.256120 1.27912 2.29750 169 657 1.78571 0.270649 1.32679 2.40338 182 687 1.86264 0.266655 1.40692 2.46596 179 687 1.93956 0.260862 1.49012 2.52456 181 700 2.03047 0.254826 1.58771 2.59671 175 708 2.13047 0.274527 1.65498 2.74258 169 710 2.24158 0.268755 1.77214 2.83537 145 710 2.35269 0.257586 1.89833 2.91581 155 710 2.46380 0.240267 2.03516 2.98273 167 719 2.63047 0.347216 2.03084 3.40714 137 724 2.83047 0.425594 2.10800 3.80055 112 724 3.03047 0.443994 2.27405 4.03849 128 724 3.23047 0.410559 2.51818 4.14424 132 730 3.73047 0.471307 2.91221 4.77864 101 730 4.23047 0.410559 3.49769 5.11677 119 - タイプ 2
- システム: IDノンパラメトリック推定値
平均累積関数表
95%正規信頼区間 時間 平均累積関数 標準誤差 下限 上限 システム 19 0.06667 0.064406 0.01004 0.44284 228 22 0.13333 0.087771 0.03670 0.48447 212 39 0.20000 0.103280 0.07269 0.55029 192 54 0.26667 0.114180 0.11521 0.61721 214 61 0.33333 0.121716 0.16295 0.68186 219 91 0.40000 0.157762 0.18465 0.86652 192 93 0.46667 0.159629 0.23869 0.91237 243 119 0.53333 0.207989 0.24834 1.14538 192 148 0.60000 0.263312 0.25386 1.41809 192 173 0.66667 0.261052 0.30945 1.43622 190 185 0.73333 0.274334 0.35227 1.52661 228 187 0.80000 0.269979 0.41289 1.55006 235 192 0.86667 0.264435 0.47658 1.57604 205 194 0.93333 0.257624 0.54335 1.60321 216 203 1.00000 0.249444 0.61330 1.63052 183 205 1.06667 0.257624 0.66442 1.71243 243 211 1.13333 0.264435 0.71738 1.79046 183 242 1.20000 0.269979 0.77210 1.86504 190 250 1.26667 0.257624 0.85023 1.88706 204 264 1.33333 0.277555 0.88664 2.00507 243 277 1.40000 0.295146 0.92615 2.11630 183 293 1.46667 0.280740 1.00786 2.13434 184 306 1.53333 0.324779 1.01238 2.32237 192 369 1.60000 0.309839 1.09468 2.33859 206 373 1.66667 0.335548 1.12325 2.47298 183 382 1.73333 0.319258 1.20810 2.48693 200 415 1.80000 0.342540 1.23962 2.61370 243 416 1.87143 0.340512 1.31007 2.67333 235 419 1.94835 0.338097 1.38662 2.73764 219 419 2.02527 0.349310 1.44435 2.83985 228 432 2.11618 0.347441 1.53391 2.91948 216 434 2.21618 0.345034 1.63337 3.00696 204 441 2.32729 0.341839 1.74512 3.10369 214 447 2.45229 0.337430 1.87262 3.21141 212 448 2.59515 0.331033 2.02109 3.33227 205 448 2.73801 0.315398 2.18466 3.43152 206 460 2.93801 0.298009 2.40832 3.58420 200 461 3.18801 0.449834 2.41776 4.20364 192 464 3.52134 0.511478 2.64893 4.68108 190 503 4.02134 0.535360 3.09778 5.22025 184 511 5.02134 0.535360 4.07443 6.18831 183 - 比較: (タイプ = 1) - (タイプ = 2)
平均累積差関数表
95%正規信頼区間 時間 平均累積差関数 標準誤差 下限 上限 19 -0.06667 0.064406 -0.19290 0.05957 22 -0.13333 0.087771 -0.30536 0.03869 33 -0.06190 0.111541 -0.28052 0.15671 39 -0.12857 0.124114 -0.37183 0.11469 54 -0.19524 0.133322 -0.45654 0.06607 61 -0.26190 0.139830 -0.53597 0.01216 88 -0.19048 0.153496 -0.49132 0.11037 91 -0.25714 0.183399 -0.61660 0.10231 93 -0.32381 0.185008 -0.68642 0.03880 119 -0.39048 0.228047 -0.83744 0.05649 148 -0.45714 0.279427 -1.00481 0.09052 173 -0.52381 0.277299 -1.06730 0.01969 185 -0.59048 0.289837 -1.15855 -0.02241 187 -0.65714 0.285719 -1.21714 -0.09714 192 -0.72381 0.280486 -1.27355 -0.17407 194 -0.79048 0.274074 -1.32765 -0.25330 203 -0.85714 0.266399 -1.37928 -0.33501 205 -0.92381 0.274074 -1.46099 -0.38663 211 -0.99048 0.280486 -1.54022 -0.44073 242 -1.05714 0.285719 -1.61714 -0.49714 250 -1.05238 0.279994 -1.60116 -0.50360 264 -1.11905 0.298435 -1.70397 -0.53413 272 -1.04762 0.302679 -1.64086 -0.45438 277 -1.11429 0.318886 -1.73929 -0.48928 287 -1.04286 0.321731 -1.67344 -0.41228 293 -1.10952 0.308568 -1.71431 -0.50474 302 -1.03810 0.310335 -1.64634 -0.42985 306 -1.10476 0.350677 -1.79208 -0.41745 317 -1.03333 0.351196 -1.72166 -0.34500 364 -0.96190 0.350677 -1.64922 -0.27459 367 -0.89048 0.349114 -1.57473 -0.20622 369 -0.95714 0.335260 -1.61424 -0.30004 373 -1.02381 0.359155 -1.72774 -0.31988 382 -1.09048 0.343985 -1.76467 -0.41628 391 -1.01905 0.355960 -1.71672 -0.32138 402 -0.94762 0.352358 -1.63823 -0.25701 415 -1.01429 0.373582 -1.74649 -0.28208 416 -1.08571 0.371724 -1.81428 -0.35715 419 -1.23956 0.379800 -1.98395 -0.49517 421 -1.16813 0.388808 -1.93018 -0.40608 431 -1.09670 0.383618 -1.84858 -0.34482 432 -1.18761 0.381917 -1.93616 -0.43907 434 -1.28761 0.379729 -2.03187 -0.54336 441 -1.39872 0.376828 -2.13729 -0.66015 444 -1.32729 0.384013 -2.07995 -0.57464 447 -1.45229 0.380094 -2.19726 -0.70733 448 -1.73801 0.360677 -2.44492 -1.03109 460 -1.93801 0.345574 -2.61532 -1.26070 461 -2.18801 0.482663 -3.13401 -1.24201 462 -2.11658 0.476966 -3.05142 -1.18174 464 -2.44991 0.535496 -3.49947 -1.40036 481 -2.37849 0.529680 -3.41664 -1.34033 498 -2.30706 0.532767 -3.35126 -1.26285 500 -2.16420 0.546276 -3.23488 -1.09352 503 -2.66420 0.568698 -3.77883 -1.54957 511 -3.66420 0.568698 -4.77883 -2.54957 548 -3.59277 0.578546 -4.72670 -2.45884 552 -3.52134 0.587608 -4.67303 -2.36965 625 -3.44991 0.604423 -4.63456 -2.26527 635 -3.37849 0.595004 -4.54467 -2.21230 650 -3.30706 0.593471 -4.47024 -2.14387 657 -3.23563 0.599884 -4.41138 -2.05988 687 -3.08178 0.595533 -4.24900 -1.91456 700 -2.99087 0.592914 -4.15296 -1.82878 708 -2.89087 0.601644 -4.07007 -1.71167 710 -2.55754 0.586803 -3.70765 -1.40743 719 -2.39087 0.638098 -3.64152 -1.14022 724 -1.79087 0.674662 -3.11319 -0.46856 730 -0.79087 0.674662 -2.11319 0.53144