生存プロット – 保険数理推定法
生存プロットでは、項目が特定時間まで正常に機能する確率が図示されます。このため、このプロットで時間の経過に伴う製品の信頼性が示されます。Y軸には生存の確率が、X軸には信頼性測度(時間、コピー数、運転マイル数)が表示されます。
ノンパラメトリック分析の場合、生存プロットは、各区間のエンドポイントでのステップを持つステップ関数になります。この例において、この関数は、保険数理推定法を使用して計算されます。
出力例
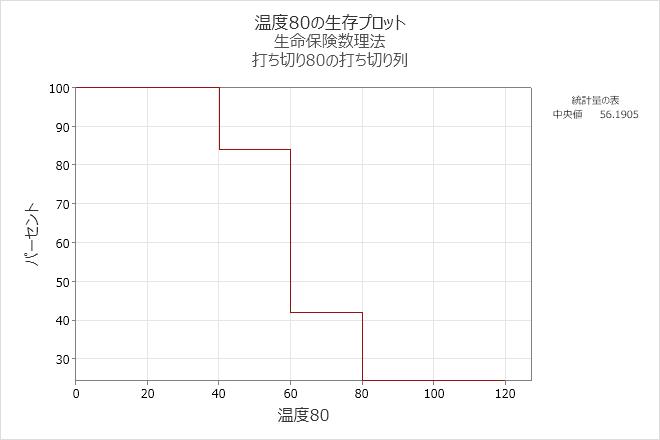
解釈
80℃で稼働しているエンジン巻揚部品の場合、60時間まで巻揚部品が正常に機能する確率は0.42です。
累積故障プロット – 保険数理推定法
累積故障プロットでは、項目が特定時間以降に故障する確率が図示されます。このため、このプロットでは、時間の経過に伴う製品の故障確率が示されます。Y軸には故障の確率が、X軸には信頼性測度(時間、コピー数、運転マイル数)が表示されます。
ノンパラメトリック分析の場合、累積故障プロットは、各区間のエンドポイントでのステップを持つステップ関数になります。この例において、この関数は、保険数理推定法を使用して計算されます。
出力例
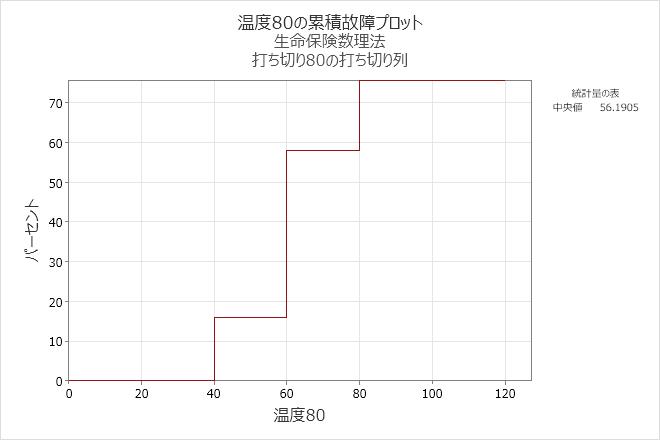
解釈
80℃で稼働しているエンジン巻揚部品の場合、60時間までに巻揚部品が故障する確率は0.58です。
ハザードプロット – 保険数理推定法
ハザード関数では、ユニットが正常に機能する時間の関数として故障尤度の測度が得られます。パラメトリック推定法を採用する場合に、ノンパラメトリックハザードプロットを使用してデータのモデル化に適した分布を判断できます。
ノンパラメトリック分析の場合、ハザードプロットは、各区間の中点でのステップを持つステップ関数になります。この例において、この関数は、保険数理推定法を使用して計算されます。
出力例
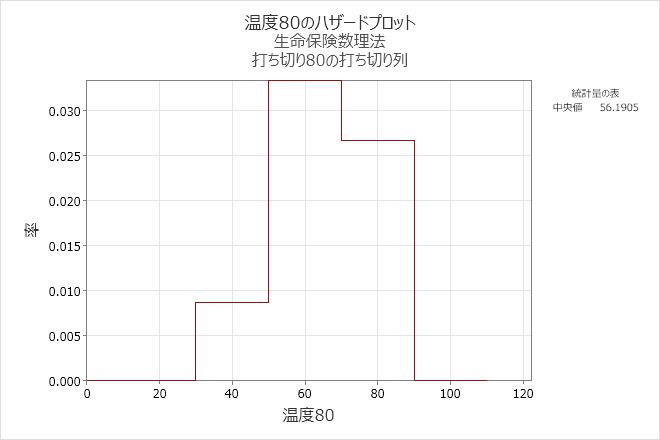
解釈
80℃で稼働しているエンジン巻揚部品の場合、ハザード関数は50~70時間の区間で増加し、70時間以降は減少します。
多重故障モードグラフ – 保険数理推定法
多重故障データでは、各故障モードのグラフが表示されます。
- 生存プロットを使用すると、品目が特定時間まで正常に機能する確率を評価できます。生存プロットでは、時間の経過に伴う製品の信頼性が示されます。
- ハザード関数を使用すると、ユニットが存続した時間の関数として故障尤度(特定時間tの短期的な故障率)を確認できます。ハザードプロットには、時間の経過に伴う故障率の傾向が示されます。
出力例
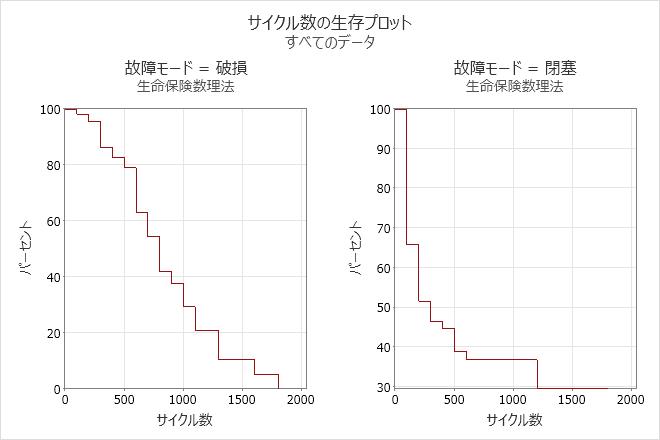
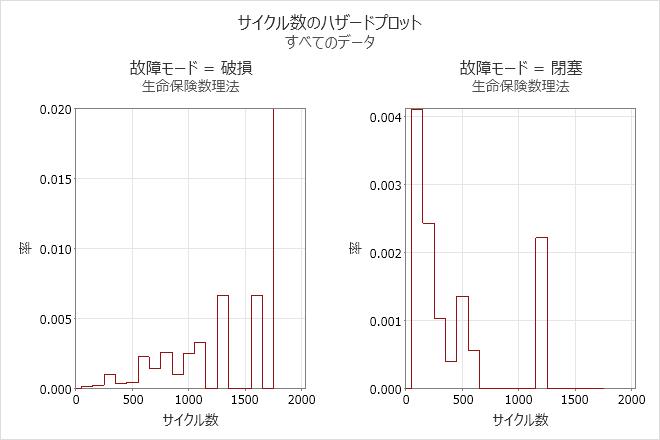
解釈
食器洗い機データの場合、スプレーアームが破損せずに200サイクルまで正常に機能する確率は95%で、閉塞せずに200サイクルまで正常に機能する確率は51%です。
破損のハザード率は、時間の経過に伴い少しずつ増加するものと考えられます。しかし、閉塞のハザード率は、時間の経過に伴い少しずつ減少するものと考えられます。
