ある信頼性エンジニアは、タービンアセンブリ用のエンジン巻揚部品の故障率を調査して、エンジン巻揚部品が故障するまでの時間を特定しようとしています。温度が高い場合、巻揚部品の分解が早くなりすぎる可能性があります。
エンジニアは80°Cおよび100°Cの故障回数を記録します。ただし、いくつかのユニットは故障する前に検定から取り除く必要があります。したがって、このデータは右打ち切りです。ノンパラメトリック分布分析(右打ち切り)を使用して以下を判断します。
- さまざまな故障率に達するまでの時間。
- さまざまな経過時間後の故障が発生していない巻揚部品の比率
- エンジン巻揚部品の生存関数(生存プロットに表示される)
- 2つの温度の生存曲線が有意に異なるかどうか
- 標本データを開く、 エンジン巻揚部品の信頼性.MWX.
- を選択します。
- 変数に、温度80温度100を入力します。
- 打ち切りをクリックします。打ち切り列を使用するに打ち切り80打ち切り100と入力します。
- 打ち切りの値に、タイプ0を入力します。OKをクリックします。
- グラフをクリックします。生存プロットを選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
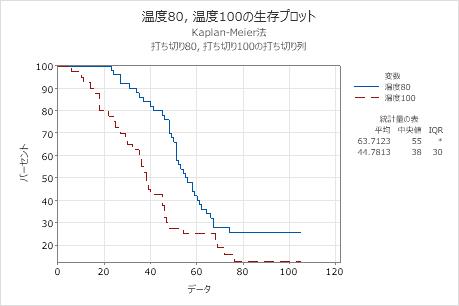
温度80での故障時間の推定中央値は55時間で、温度100での故障時間の推定中央値は38時間です。このため、温度が上がると、約17時間で故障時間の中央値が低下します。
生存確率の推定値は、Kaplan-Meier推定表に表示されます。80℃では、0.9000(90%)のエンジン巻揚部品が31時間以上正常に機能します。100℃では、0.9000(90%)のエンジン巻揚部品が14時間以上正常に機能します。
検定統計量の表では、p値 < α(通常α = 0.05)の場合は、生存曲線が有意に異なることを示します。この場合、p値(0.005および0.000)はともにα未満となり、20℃の変化でエンジン巻揚部品の故障に影響があることを示します。
- 80° C
- 変数: 温度80
打ち切り
打ち切り情報 計数 打ち切られていない値 37 右打ち切り値 13 ノンパラメトリック推定値変数の特性
95.0%正規信頼区間 平均 (MTTF) 標準誤差 下限 上限 Q1 中央値 Q3 四分位間範囲 63.7123 3.83453 56.1968 71.2279 48 55 * * Kaplan-Meier推定
95.0%正規信頼区間 時間 リスクにさらされた件数 故障数 生存確率 標準誤差 下限 上限 23 50 1 0.980000 0.0197990 0.941195 1.00000 24 49 1 0.960000 0.0277128 0.905684 1.00000 27 48 2 0.920000 0.0383667 0.844803 0.99520 31 46 1 0.900000 0.0424264 0.816846 0.98315 34 45 1 0.880000 0.0459565 0.789927 0.97007 35 44 1 0.860000 0.0490714 0.763822 0.95618 37 43 1 0.840000 0.0518459 0.738384 0.94162 40 42 1 0.820000 0.0543323 0.713511 0.92649 41 41 1 0.800000 0.0565685 0.689128 0.91087 45 40 1 0.780000 0.0585833 0.665179 0.89482 46 39 1 0.760000 0.0603987 0.641621 0.87838 48 38 3 0.700000 0.0648074 0.572980 0.82702 49 35 1 0.680000 0.0659697 0.550702 0.80930 50 34 1 0.660000 0.0669925 0.528697 0.79130 51 33 4 0.580000 0.0697997 0.443195 0.71680 52 29 1 0.560000 0.0701997 0.422411 0.69759 53 28 1 0.540000 0.0704840 0.401854 0.67815 54 27 1 0.520000 0.0706541 0.381521 0.65848 55 26 1 0.500000 0.0707107 0.361410 0.63859 56 25 1 0.480000 0.0706541 0.341521 0.61848 58 24 2 0.440000 0.0701997 0.302411 0.57759 59 22 1 0.420000 0.0697997 0.283195 0.55680 60 21 1 0.400000 0.0692820 0.264210 0.53579 61 20 1 0.380000 0.0686440 0.245460 0.51454 62 19 1 0.360000 0.0678823 0.226953 0.49305 64 18 1 0.340000 0.0669925 0.208697 0.47130 66 17 1 0.320000 0.0659697 0.190702 0.44930 67 16 2 0.280000 0.0634980 0.155546 0.40445 74 13 1 0.258462 0.0621592 0.136632 0.38029 - 100° C
- 変数: 温度100
打ち切り
打ち切り情報 計数 打ち切られていない値 34 右打ち切り値 6 ノンパラメトリック推定値変数の特性
95.0%正規信頼区間 平均 (MTTF) 標準誤差 下限 上限 Q1 中央値 Q3 四分位間範囲 44.7813 4.43366 36.0914 53.4711 24 38 54 30 Kaplan-Meier推定
95.0%正規信頼区間 時間 リスクにさらされた件数 故障数 生存確率 標準誤差 下限 上限 6 40 1 0.97500 0.0246855 0.926617 1.00000 10 39 1 0.95000 0.0344601 0.882459 1.00000 11 38 1 0.92500 0.0416458 0.843376 1.00000 14 37 1 0.90000 0.0474342 0.807031 0.99297 16 36 1 0.87500 0.0522913 0.772511 0.97749 18 35 3 0.80000 0.0632456 0.676041 0.92396 22 32 1 0.77500 0.0660256 0.645592 0.90441 24 31 1 0.75000 0.0684653 0.615810 0.88419 25 30 1 0.72500 0.0706001 0.586626 0.86337 27 29 1 0.70000 0.0724569 0.557987 0.84201 29 28 1 0.67500 0.0740566 0.529852 0.82015 30 27 1 0.65000 0.0754155 0.502188 0.79781 32 26 1 0.62500 0.0765466 0.474972 0.77503 35 25 1 0.60000 0.0774597 0.448182 0.75182 36 24 2 0.55000 0.0786607 0.395828 0.70417 37 22 1 0.52500 0.0789581 0.370245 0.67975 38 21 2 0.47500 0.0789581 0.320245 0.62975 39 19 1 0.45000 0.0786607 0.295828 0.60417 40 18 1 0.42500 0.0781625 0.271804 0.57820 45 17 2 0.37500 0.0765466 0.224972 0.52503 46 15 2 0.32500 0.0740566 0.179852 0.47015 47 13 1 0.30000 0.0724569 0.157987 0.44201 48 12 1 0.27500 0.0706001 0.136626 0.41337 54 11 1 0.25000 0.0684653 0.115810 0.38419 68 8 1 0.21875 0.0666585 0.088102 0.34940 69 7 1 0.18750 0.0640434 0.061977 0.31302 72 6 1 0.15625 0.0605154 0.037642 0.27486 76 5 1 0.12500 0.0559017 0.015435 0.23457 - 生存曲線の比較
検定統計量
方法 カイ二乗 自由度 p値 Log-Rank 7.7152 1 0.005 Wilcoxon 13.1326 1 0.000