このトピックの内容
カプラン-マイヤー推定法
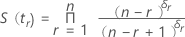
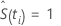
S(t0) = 1およびt0 = 0の場合。
経験ハザード関数
ハザード関数は、ある区間での故障率を示します。ハザード関数は、最初の打ち切りの観測値より前では0です。打ち切りなしの観測値でのみ、ハザード関数は変化します。最後の打ち切りなしのデータ点以降、ハザード関数はプロットされません。

同順位がある場合、同順位の最大順位を使用してハザード関数を推定します。詳細については、ネルソン1を参照してください。
故障までの平均時間
打ち切りなしデータの場合、故障までの平均時間は、平均故障時間と同じになります。打ち切りまたは打ち切りなしデータに使用される一般的な計算式は次のとおりです。
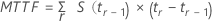
また、最大観測値が打ち切られている場合、打ち切りなしの最大観測値の時間を、計算対象の時間制限として扱います。詳細については、リー2を参照してください。
故障までの平均時間(MTTF)の標準誤差
故障までの平均時間の標準誤差は、分散の平方根です。すべての観測値が打ち切りなしの場合、不偏推定値が計算されます。
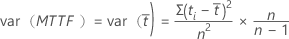
一部のデータが打ち切られている場合、分散の不偏推定値は次の計算式になります。

経験ハザード関数の形状により、生存曲線下の領域Arは、縦が生存関数と、横が打ち切りなしの観測値の区間と同等になる長方形になります。
表記
| 用語 | 説明 |
|---|---|
| tr | 順位rでのデータ点の時間 |
| r | データ点の順位。最初の故障は低順位になる |
| n | 合計個数 |
| δr | j番目の観測値が打ち切りの場合は0、j番目の観測値が打ち切りなしの場合は1になる |
| c | 次の打ち切りなしの観測値までのデータ点の数 |
| S(tr) | 時間trでの経験生存関数 |
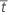 | 平均故障ストレス |
| Ar | 生存曲線下のtrの右側の領域 |
| m | 打ち切りなしの観測値の合計数 |
参考文献
1. W. Nelson(1982年)『Applied Life Data Analysis』133頁、John Wiley & Sons, Inc
2. Elisa T. Lee(1992年)『Statistical Methods for Survival Data Analysis』第2版、73~76頁、John Wiley & Sons, Inc
保険数理推定法
保険数理モデルは、故障時間のグループに関する情報を表示する別のノンパラメトリック分析です。カプラン-マイヤー法では、故障が発生すると、その区間の最後に停止すると仮定されます。Minitabの保険数理モデルは、区間の中央で停止が発生すると仮定して、これにより区間内で機能しているユニット数の減少に影響を及ぼします。保険数理法を使用する生存関数の推定値は次のとおりです。
 i = 0の場合
i = 0の場合
 i > 0の場合
i > 0の場合
経験ハザード関数
ハザード関数は、ある区間での故障率を示します。保険数理法で、区間の中点を求めるために計算するものと仮定します。ハザードプロットで、関数は中点から中点に図示されます。詳細については、「表記」セクションの次の「参考文献」を参照してください。
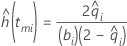
表記
| 用語 | 説明 |
|---|---|
| ni | 区間内のユニット数 |
| di | 区間内の故障数 |
| n'i |  |
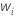 | 区間内の打ち切り数 |
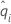 | 事象の条件付き確率 = di/n'i |
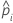 |  |
| tmi | 保険数理区間の中点の時間 |
| bi | 保険数理区間の長さ |
参考文献
Collett, D.(1994年)『Modelling Survival Data in Medical Research』Chapman and Hall
Lee, Elisa T.(1992年)『Statistical Methods for Survival Data Analysis』第2版、John Wiley & Sons
ターンブル推定法
ターンブル1, 2によって、データの累積分布関数のノンパラメトリック最尤推定値を計算するために、ノンパラメトリック反復アルゴリズムが開発されました。この方法は、区間が重複している場合など、より一般的な状況に適用します。
区間確率のターンブル推定値を要約する出力が、これらの確率の標準誤差とともに表示されます。
参考文献
- B.W. Turnbull(1976年)「The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data」『Journal of the Royal Statistical Society』第38巻、290~295頁
- B.W. Turnbull(1974年)「Nonparametric Estimation of a Survivorship Function with Doubly Censored Data」『Journal of the American Statistical Association』第69巻、345合、169~173頁
信頼区間
推定法に関係なく、Minitabでは信頼区間の計算に正規近似を使用します。信頼区間は次のとおりです。
計算式
生存確率の推定値  zα × 推定値の標準誤差
zα × 推定値の標準誤差
表記
| 用語 | 説明 |
|---|---|
| zα | 管理図の中でも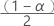 標準正規分布の上限棄却値 標準正規分布の上限棄却値 |
| α | 信頼水準 |
