指定された2つの分布パラメータ
μおよびσ(ワイブルモデルではθおよびβ)に計画値を指定すると、百分位数や信頼性が計算されます。
- p番目の百分位数の計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティックおよび極値)の場合

- 対数-位置-尺度モデル(ワイブル、対数正規、対数ロジスティック)の場合

- 位置-尺度モデル(正規、ロジスティックおよび極値)の場合
- 指定された時間での信頼性の計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティック、極値)の場合

- 対数-位置-尺度モデル(ワイブル、対数正規、対数ロジスティック)の場合

- 位置-尺度モデル(正規、ロジスティック、極値)の場合
表記
| 用語 | 説明 |
|---|---|
| μ | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック) |
| σ | 尺度パラメータ |
| θ | ワイブルの尺度パラメータ |
| β | ワイブルの形状パラメータ |
| t | 時間 |
| tp,plan | 時間tでのp番目の百分位数の計画値 |
| Rplan(t) | 時間tでの信頼性の計画値 |
| Φ | 対応する分布のCDF |
| Φ-1 | 対応する分布の逆CDF |
指定された百分位数と尺度(または形状)
β(またはσ)に計画値、百分位数tp0を指定する場合、μの計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティックおよび最小極値)の場合
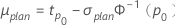
- 対数-位置-尺度モデル(ワイブル、対数正規、および対数ロジスティック)の場合

百分位数または信頼性の計画値を得るには、2つのパラメータを指定する際の計算を使用します。詳細については、セクション「指定された2つの分布パラメータ」を参照してください。
表記
| 用語 | 説明 |
|---|---|
| μ | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック) |
| μplan | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック)の計画値 |
| σ | 尺度パラメータ |
| σplan | 尺度パラメータの計画値 |
| β | ワイブルの形状パラメータ |
| t | 時間 |
| tp | 時間tでの百分位数 |
| Φ-1 | 対応する分布の逆CDF |
指定された百分位数と尺度(または位置)
μ(またはθ)に計画値、百分位数tp0を指定する場合、σの計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティックおよび最小極値)の場合
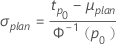
- 対数-位置-尺度モデル(ワイブル、対数正規、および対数ロジスティック)の場合
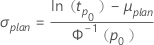
百分位数または信頼性の計画値を得るには、2つのパラメータを指定する際の計算を使用します。詳細については、セクション「指定された2つの分布パラメータ」を参照してください。
表記
| 用語 | 説明 |
|---|---|
| μ | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック) |
| μplan | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック)の計画値 |
| σ | 尺度パラメータ |
| σplan | 尺度パラメータの計画値 |
| β | ワイブルの形状パラメータ |
| t | 時間 |
| tp | 時間tでの百分位数 |
| Φ-1 | 対応する分布の逆CDF |
指定された2つの百分位数
2つの百分位数に計画値を指定する場合、μとσ両方の計画値を計算します。
- μの計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティックおよび最小極値)の場合
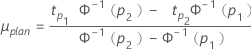
- 対数-位置-尺度モデル(ワイブル、対数正規、対数ロジスティック)の場合
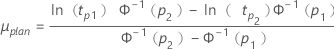
- 位置-尺度モデル(正規、ロジスティックおよび最小極値)の場合
- σの計画値は次のようにして計算します。
- 位置-尺度モデル(正規、ロジスティック、最小極値)の場合
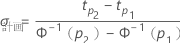
- 対数-位置-尺度モデル(ワイブル、対数正規、対数ロジスティック)の場合
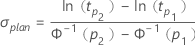
- 位置-尺度モデル(正規、ロジスティック、最小極値)の場合
百分位数または信頼性の計画値を得るには、2つのパラメータを指定する際の計算を使用します。詳細については、セクション「指定された2つの分布パラメータ」を参照してください。
表記
| 用語 | 説明 |
|---|---|
| μ | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック) |
| μplan | 平均(正規、ロジスティック)、位置(最小極値)、または対数-位置(対数正規、対数ロジスティック)の計画値 |
| σ | 尺度パラメータ |
| σplan | 尺度パラメータの計画値 |
| β | ワイブルの形状パラメータ |
| t | 時間 |
| tp | 時間tでの百分位数 |
| Φ-1 | 対応する分布の逆CDF |
