確率プロット
確率プロットには、次の要素が含まれます。
- プロット点 - 大きさの順に並べたデータセットの確率に対応する推定百分位数です。
- 適合線 - パラメータの最尤推定値に基づいて分布で期待される百分位数です。
- 信頼区間 - 百分位数の信頼区間です。
プロット点は特定の分布には依存しないので、どの確率プロットを作成した場合も、変換前であればプロット点は同じです。ただし、適合線は選択するパラメトリック分布によって異なります。したがって、確率プロットを使用して、特定の分布がデータにあてはまるかどうかを評価することができます。一般的に、点の位置が適合線に近ければ、適合度が高いといえます。
プロット点
確率プロットのプロット点は、時間t以前に製品が故障する可能性を表します。右打ち切りまたは打ち切りなしのデータの場合、次の方法でプロット点を計算します。
- 中央値順位法(デフォルト)
- 修正されたKaplan-Meier法
- Herd-Johnson法
- Kaplan-Meier法
データに同順位の故障時間(同一の故障時間)が含まれる場合、すべての点(デフォルト)、平均(中央値)、または同順位点の最大値のいずれかがプロットされます。同順位に故障や停止が含まれる場合、故障は停止より前に発生したものとみなされます。
これらの方法のそれぞれが、F(t)のノンパラメトリック推定値、故障までの時間であるランダム変数Tの累積分布関数を生成します。
観測値n個のサンプルの場合、x(1), x(2),..., x(n)と順番の統計値にするか、昇順にデータを並べます。そのとき、iは順番に並んだ観測値x(I)のI番目の順位を示します。各方法の計算式は次のとおりです。
中央値順位(Benardの方法)
打ち切りなしデータの計算式
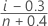
打ち切りありデータの計算式

修正されたKaplan-Meier
打ち切りなしデータの計算式
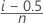
打ち切りありデータの計算式
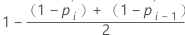
Herd-Johnson推定
打ち切りなしデータの計算式

打ち切りありデータの計算式
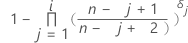
Kaplan-Meier製品限界推定
注
最大観測値が打ち切りなしの場合、Kaplan-Meier法は、最大打ち切りなし観測値に対してp = 1の結果となります。このケースでは、最大観測値のKaplan-Meier推定は、プロットで使用できない数になります。この問題は、最大値pをpと1の距離の90%として再計算することで訂正されます。
注
任意打ち切りのデータの場合、Turnbull法1を使用して累積確率が推定されます。
打ち切りなしデータの計算式

打ち切りありデータの計算式
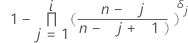
表記
| 用語 | 説明 |
|---|---|
| i | 連続順位で指定された同順位を持つデータ点の順位 |
| n | データに含まれる観測値の数 |
| δj | j番目の観測値が打ち切りの場合0、j番目の観測値が打ち切りなしの場合1になります |
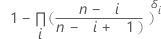
| ARi |
 |
| AR0 | =0 |
| p'i |
 |
適合線
次の表は、適合線のx座標とy座標がどのように構築されているか示しています。次の内容に注意してください。
- ワイブル分布、3-パラメータワイブル分布、指数分布、対数正規分布、または対数ロジスティック分布を使用している場合、対数尺度にx軸が変換されます。
- デフォルトではパーセント尺度にy軸が変換されます。Y-スケールタイプを確率に変更する場合、y軸が確率尺度に変換されます。
| 分布 | x座標 | y座標 |
|---|---|---|
| 最小極値 | 故障時間 | ln(–ln(1 – p)) |
| ワイブル | ln(故障時間) | ln(–ln(1 – p)) |
| 3-パラメータワイブル | ln(故障時間 – しきい値) | ln(–ln(1 – p)) |
| 指数 | ln(故障時間) | ln(–ln(1 – p)) |
| 2-パラメータ指数 | ln(故障時間 – しきい値) | ln(–ln(1 – p)) |
| 正規 | 故障時間 | Φ –1(p) |
| 対数正規 | ln(故障時間) | Φ –1(p) |
| 3-パラメータ対数正規 | ln(故障時間 – しきい値) | Φ –1(p) |
| ロジスティック | 故障時間 |
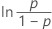 |
| 対数ロジスティック | ln(故障時間) |
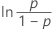 |
| 3-パラメータ対数ロジスティック | ln(故障時間 – しきい値) |
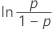 |
表記
| 用語 | 説明 |
|---|---|
| Φ –1 | 標準正規分布の逆累積分布関数(ICDF) |
| ln(x) | xの自然対数 |
1 B.W. Turnbull(1976)『The Empirical Distribution Function with Arbitrarily Grouped, Censored and Truncated Data』、Journal of the Royal Statistical Society, 38, 290-295.
