カプラン-マイヤー推定は、製品限界推定としても知られており、複数の故障や停止があるノンパラメトリックデータセットの生存確率の計算に使用できます。推定に使用する式は次のとおりです。
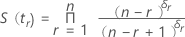
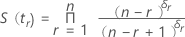
S(t0) = 1およびt0 = 0の場合。
経験ハザード関数
ハザード関数は、ある区間での故障率を示します。ハザード関数は、最初の打ち切りの観測値より前では0です。打ち切りなしの観測値でのみ、ハザード関数は変化します。最後の打ち切りなしのデータ点以降、ハザード関数はプロットされません。

同順位がある場合、同順位の最大順位を使用してハザード関数を推定します。詳細については、ネルソン1を参照してください。
故障までの平均時間
打ち切りなしデータの場合、故障までの平均時間は、平均故障時間と同じになります。打ち切りまたは打ち切りなしデータに使用される一般的な計算式は次のとおりです。
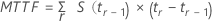
また、最大観測値が打ち切られている場合、打ち切りなしの最大観測値の時間を、計算対象の時間制限として扱います。詳細については、リー2を参照してください。
故障までの平均時間(MTTF)の標準誤差
故障までの平均時間の標準誤差は、分散の平方根です。すべての観測値が打ち切りなしの場合、不偏推定値が計算されます。
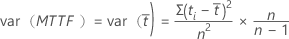
一部のデータが打ち切られている場合、分散の不偏推定値は次の計算式になります。

経験ハザード関数の形状により、生存曲線下の領域Arは、縦が生存関数と、横が打ち切りなしの観測値の区間と同等になる長方形になります。
表記
| 用語 | 説明 |
|---|---|
| tr | 順位rでのデータ点の時間 |
| r | データ点の順位。最初の故障は低順位になる |
| n | 合計個数 |
| δr | j番目の観測値が打ち切りの場合は0、j番目の観測値が打ち切りなしの場合は1になる |
| c | 次の打ち切りなしの観測値までのデータ点の数 |
| S(tr) | 時間trでの経験生存関数 |
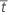 | 平均故障ストレス |
| Ar | 生存曲線下のtrの右側の領域 |
| m | 打ち切りなしの観測値の合計数 |
参考文献
1. W. Nelson(1982年)『Applied Life Data Analysis』133頁、John Wiley & Sons, Inc
2. Elisa T. Lee(1992年)『Statistical Methods for Survival Data Analysis』第2版、73~76頁、John Wiley & Sons, Inc
