このトピックの内容
パラメータ推定値
計算式
| 分布 | パラメータ |
|---|---|
|
最小極値 正規 ロジスティック |
μ = 位置、 σ = 尺度、σ > 0 |
|
対数正規 対数ロジスティック |
μ = 位置、μ > 0 σ = 尺度、 σ > 0 |
|
3-パラメータ対数正規 3-パラメータ対数ロジスティック |
μ = 位置、μ > 0 σ = 尺度、σ > 0 λ = しきい値、 |
|
ワイブル |
α = 尺度、α = 指数（μ） β = 形状、β = 1/σ |
|
3-パラメータワイブル |
α = 尺度、α = 指数（μ） β = 形状、β = 1/σ λ = しきい値、 |
|
指数 |
θ = 尺度、θ > 0 |
|
2-パラメータ指数 |
θ = 尺度、θ > 0 λ = しきい値、 |
パラメータ推定値の標準誤差
標準誤差は、パラメータ推定値の標準偏差です。標準誤差で各推定値における変動性の推定法を使用できます。
、
、
、
、
、および
は、μ、σ、α、β、θ、およびλのMLEの標準誤差を示します。各標準誤差は、Fisher情報行列の逆行列の適切な対角要素の平方根で計算されます。
パラメータ推定値に対する信用限界
計算式
| 分布 | パラメータ | 下側信頼限界 | 上側信頼限界 |
|---|---|---|---|
| 最小極値、正規、ロジスティック、対数正規、対数ロジスティック | 位置、μ |
 |
 |
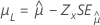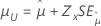| 尺度、σ |
 |
 |
|
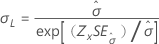| 3-パラメータ対数正規、3-パラメータ対数ロジスティック | 位置、μ |
 |
 |
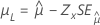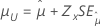| 尺度、σ |
 |
 |
|
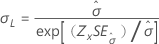| しきい値、λ |
 |
 |
|
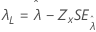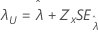| ワイブル | 形状、β |
 |
 |
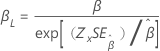| 尺度、α |
 |
 |
|
|
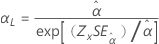3-パラメータワイブル |
形状、β |
 |
 |
|
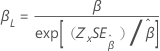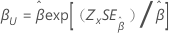尺度、α |
 |
 |
|
|
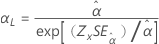しきい値、λ |
 |
 |
|
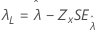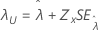| 指数 | 尺度 |
 |
 |
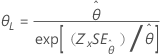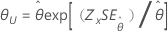| 2-パラメータ指数 | 尺度、θ |
 |
 |
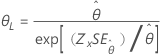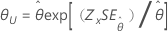| しきい値、λ |
 |
 |
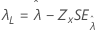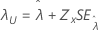注
いくつかのデータでは、尤度関数が制限されていないため、しきい値パラメータ（2-パラメータ指数など）と整合していない分布の推定値が算出されます。この状況では、推定されたパラメータの分散-共分散行列で数値的に判断できません。その場合、Minitabによって次の内容が仮定されます。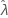
は固定値で、次のとおりになります。SE（
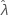） = 0。次の上限および下限
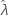は
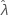です。
表記
| 用語 | 説明 |
|---|---|
| zx | 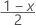 の標準正規分布の上限棄却値（100x%が信頼水準かつ0 < x < 1の場合）。 |
