確率プロットを使用すると、一般的な分布の適合度を比較して、最適適合分布を選択できます。データ点が確率プロットの比較的直線上にある場合、その分布を使用してデータをモデル化するのが妥当であると結論付けられます。したがって、最適適合分布とは、点が最も緊密に適合線に従っている分布を指します。
プロット上の点は、ノンパラメトリック法に基づく故障の推定百分位数です。ポインターをデータ点上に置くと、観測された故障時間と推定累積確率が表示されます。
直線は適合分布に基づいています。この例では、ワイブル、対数正規、指数、正規が適合分布です。ポインターを適合線上に置くと、各種パーセントの百分位数表が表示されます。
最尤推定法(MLE)の場合、Anderson-Darling(adj)統計量を表示して、各分布の適合度を評価します。
最小二乗(LSXY)推定法を使用すると、1以下の正の数になるピアソン相関係数を表示します。相関係数の値が高ければ、分布がうまく適合していることを示します。
注
Anderson-Darling(adj)統計量の解釈に関する詳細については、「適合度」を参照してください。
出力例
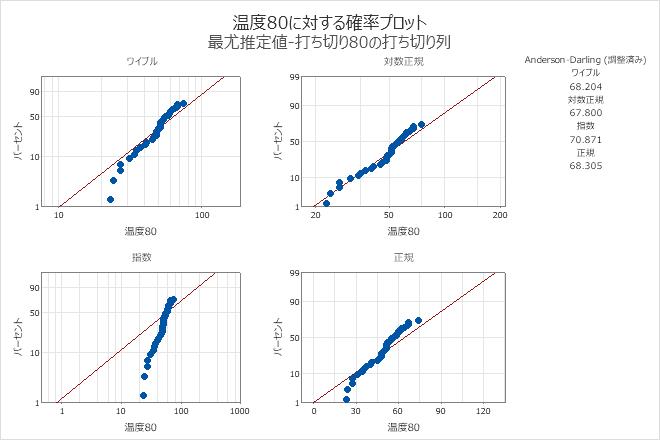
解釈
エンジン巻揚部品データの場合、確率プロットには、ワイブル分布および対数正規分布が指数分布や正規分布と比べてよりデータに適合していることが示されています。対数正規分布が、これらのデータに最も適合していることがわかります。
