ある信頼性エンジニアは、タービンアセンブリ用のエンジン巻揚部品の故障率を調査して、エンジン巻揚部品が故障するまでの時間を特定しようとしています。温度が高い場合、巻揚部品の分解が早くなりすぎる可能性があります。
エンジニアはさまざまな温度でのエンジン巻揚部品の故障回数を記録します。ただし、いくつかのユニットは故障する前に検定から取り除く必要があります。したがって、このデータは右打ち切りです。80°Cで収集されたデータの分布モデルを選択するため、分布識別プロット(右打ち切り)を使用します。
- サンプルデータを開く、 エンジン巻揚部品の信頼性.MWX.
- を選択します。
- 変数に、温度80を入力します。
- 分布を指定を選択します。デフォルトの分布(ワイブル、対数正規、指数、および正規)が選択されていることを確認してください。
- 打ち切りをクリックします。打ち切り列を使用するに打ち切り80と入力します。
- 打ち切りの値に0を入力します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
故障時間の点は、対数正規確率プロットでほぼ直線上に収まります。このため、対数正規分布がうまくあてはまります。このようにして、エンジニアは80℃で収集したデータをモデル化するために対数正規分布の使用を決定します。
Minitabは、百分位数の表と平均故障時間(MTTF、mean time to failure)の表も示し、分布ごとに計算された故障時間を提示します。その計算値を比較して、異なる分布で結果がどのように変化するか確認できます。いくつかの分布がデータにうまくあてはまる場合は、最も保守的な結果を提供する分布を使用できます。
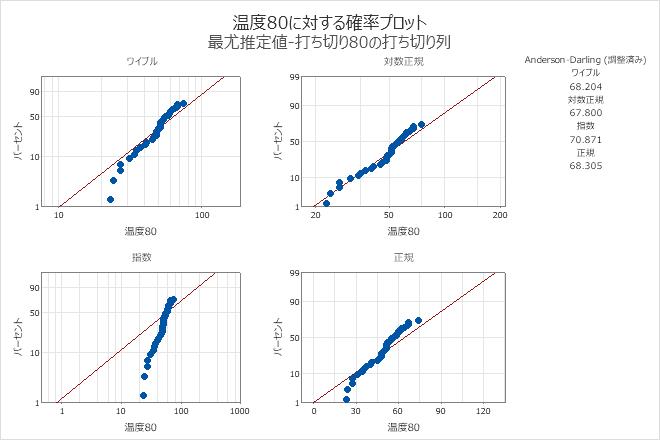
適合度
| 分布 | Anderson-Darling (調整済み) |
|---|---|
| ワイブル | 68.204 |
| 対数正規 | 67.800 |
| 指数 | 70.871 |
| 正規 | 68.305 |
パーセンタイル表
| 95%正規信頼区間 | |||||
|---|---|---|---|---|---|
| 分布 | パーセント | パーセンタイル | 標準誤差 | 下限 | 上限 |
| ワイブル | 1 | 10.0765 | 2.78453 | 5.86263 | 17.3193 |
| 対数正規 | 1 | 19.3281 | 2.83750 | 14.4953 | 25.7722 |
| 指数 | 1 | 0.809731 | 0.133119 | 0.586684 | 1.11758 |
| 正規 | 1 | -0.549323 | 8.37183 | -16.9578 | 15.8592 |
| ワイブル | 5 | 20.3592 | 3.79130 | 14.1335 | 29.3273 |
| 対数正規 | 5 | 26.9212 | 3.02621 | 21.5978 | 33.5566 |
| 指数 | 5 | 4.13258 | 0.679391 | 2.99422 | 5.70371 |
| 正規 | 5 | 18.2289 | 6.40367 | 5.67790 | 30.7798 |
| ワイブル | 10 | 27.7750 | 4.11994 | 20.7680 | 37.1463 |
| 対数正規 | 10 | 32.1225 | 3.09409 | 26.5962 | 38.7970 |
| 指数 | 10 | 8.48864 | 1.39552 | 6.15037 | 11.7159 |
| 正規 | 10 | 28.2394 | 5.48103 | 17.4968 | 38.9820 |
| ワイブル | 50 | 62.6158 | 4.62515 | 54.1763 | 72.3700 |
| 対数正規 | 50 | 59.8995 | 4.31085 | 52.0192 | 68.9735 |
| 指数 | 50 | 55.8452 | 9.18089 | 40.4622 | 77.0766 |
| 正規 | 50 | 63.5518 | 4.06944 | 55.5759 | 71.5278 |
MTTF表
| 95%正規信頼区間 | ||||
|---|---|---|---|---|
| 分布 | 平均 | 標準誤差 | 下限 | 上限 |
| ワイブル | 64.9829 | 4.6102 | 56.5472 | 74.677 |
| 対数正規 | 67.4153 | 5.5525 | 57.3656 | 79.225 |
| 指数 | 80.5676 | 13.2452 | 58.3746 | 111.198 |
| 正規 | 63.5518 | 4.0694 | 55.5759 | 71.528 |
