ある信頼性エンジニアが、新しいタイプのマフラーの信頼性を評価し、50,000マイル保証に対して予想される保証請求の比率を推定します。エンジニアは古いタイプのマフラーと新しいタイプのマフラー両方の故障データを収集します。マフラーは、故障がないかどうか10,000マイルごとに点検されました。
エンジニアは10,000マイルごとの故障数を記録します。したがって、このデータは任意打ち切りです。パラメトリック分布分析(任意打ち切り)を使用して新しいマフラーの故障データを分析する前に、分布識別プロット(任意打ち切り)を使用して分析の分布モデルを選択します。
- サンプルデータを開く、 マフラーの信頼性.MWX.
- を選択します。
- 開始変数に、開始(新)を入力します。
- 終了変数に、終了(新)を入力します。
- 度数列 (オプション)に、度数(新)を入力します。
- 分布を指定を選択します。デフォルトの分布(ワイブル、対数正規、指数、および正規)が選択されていることを確認してください。
- OKをクリックします。
結果を解釈する
ワイブル確率プロットでは、点がほぼ直線上に収まります。このため、ワイブル分布がうまくあてはまります。このようにして、エンジニアはパラメトリック分布分析(任意打ち切り)のデータをモデル化するためにワイブル分布の使用を決定します。
Minitabは、百分位数の表と平均故障時間(MTTF、mean time to failure)の表も示し、分布ごとに計算された故障時間を提示します。その計算値を比較して、異なる分布で結果がどのように変化するか確認できます。いくつかの分布がデータにうまくあてはまる場合は、最も保守的な結果を提供する分布を使用できます。
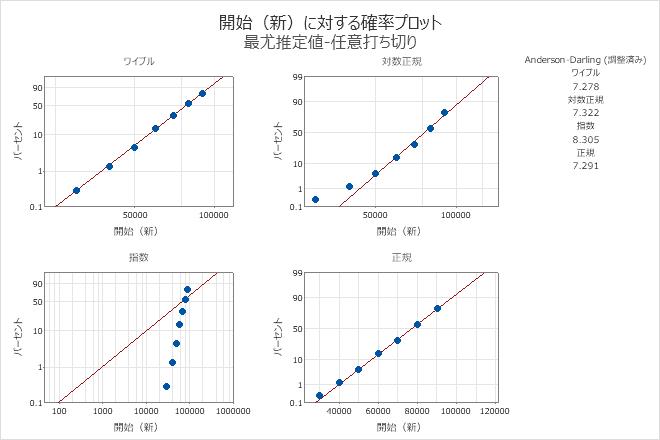
度数(新)の度数を使用します
適合度
| 分布 | Anderson-Darling (調整済み) |
|---|---|
| ワイブル | 7.278 |
| 対数正規 | 7.322 |
| 指数 | 8.305 |
| 正規 | 7.291 |
パーセンタイル表
| 95%正規信頼区間 | |||||
|---|---|---|---|---|---|
| 分布 | パーセント | パーセンタイル | 標準誤差 | 下限 | 上限 |
| ワイブル | 1 | 37265.1 | 938.485 | 35470.3 | 39150.6 |
| 対数正規 | 1 | 43817.7 | 688.033 | 42489.7 | 45187.2 |
| 指数 | 1 | 941.789 | 32.5296 | 880.143 | 1007.75 |
| 正規 | 1 | 39810.3 | 1047.34 | 37757.6 | 41863.1 |
| ワイブル | 5 | 49434.9 | 841.147 | 47813.5 | 51111.3 |
| 対数正規 | 5 | 51458.9 | 624.451 | 50249.5 | 52697.5 |
| 指数 | 5 | 4806.55 | 166.019 | 4491.93 | 5143.21 |
| 正規 | 5 | 50694.9 | 810.524 | 49106.3 | 52283.5 |
| ワイブル | 10 | 56006.1 | 759.186 | 54537.7 | 57514.0 |
| 対数正規 | 10 | 56063.1 | 585.905 | 54926.4 | 57223.3 |
| 指数 | 10 | 9873.05 | 341.017 | 9226.79 | 10564.6 |
| 正規 | 10 | 56497.5 | 699.183 | 55127.1 | 57867.8 |
| ワイブル | 50 | 77639.9 | 501.312 | 76663.5 | 78628.7 |
| 対数正規 | 50 | 75850.3 | 576.625 | 74728.5 | 76988.9 |
| 指数 | 50 | 64952.9 | 2243.49 | 60701.3 | 69502.3 |
| 正規 | 50 | 76966.0 | 514.756 | 75957.1 | 77974.9 |
MTTF表
| 95%正規信頼区間 | ||||
|---|---|---|---|---|
| 分布 | 平均 | 標準誤差 | 下限 | 上限 |
| ワイブル | 76585.0 | 488.71 | 75633.1 | 77549 |
| 対数正規 | 77989.9 | 615.96 | 76792.0 | 79207 |
| 指数 | 93707.3 | 3236.67 | 87573.5 | 100271 |
| 正規 | 76966.0 | 514.76 | 75957.1 | 77975 |
