試験時間
再計画したシステムが大幅に改良されたことを実証するための最低成分数Nにかかる各システムの試験時間は、100(1 – α)%の信頼水準で次のように計算されます。
- m = 0(0-故障試験計画)の場合

- m > 0(m-故障試験計画)の場合
Rを求める式を解きます(実証試験計画における故障試験計画の方法と計算式の「式」セクションを参照してください。そして、tを次のようにします。
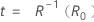
表記
| 用語 | 説明 |
|---|---|
| t | 時間 |
| m | 故障数 |
| α | 有意水準(アルファ)、1と等しい – 信頼水準 |
| N | 試験する最低成分数 |
| R0 | 区間(0、1)に限定した解 |
| R–1(t) | 逆信頼性関数 |
サンプルサイズ
再計画したシステムが大幅に改良されたことを実証するための最低システム数は、100(1 – α)%の信頼水準で次のように計算されます。
- m = 0(0-故障試験計画)の場合

- m > 0(m-故障試験計画)の場合
Nを求める式を解きます(実証試験計画における故障試験計画の方法と計算式の「式」セクションを参照してください。次を開始値とする。
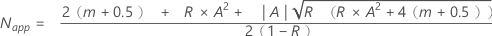

表記
| 用語 | 説明 |
|---|---|
| t | 時間 |
| m | 故障数 |
| α | 有意水準(アルファ)、1と等しい – 信頼水準 |
| N | 試験する最低システム数 |
| R(t) | 信頼性関数 |
| R–1(t) | 逆信頼性関数 |
