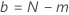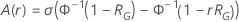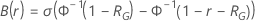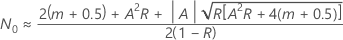試験計画に合格する確率の計算は、故障をモデル化する分布によって異なります。対数-位置-尺度分布の場合、確率は改善比の関数です。位置-尺度分布の場合、確率は改善量の関数です。計算式は、サンプルサイズを指定するか、または試験時間を指定するかによって、2つのケースに分割されます。
サンプルサイズ
実証試験の規格にサンプルサイズが含まれている場合、合格する確率の計算には試験時間が必要です。与えられたサンプルサイズで、 信頼水準は次の式を満たします:
信頼水準は次の式を満たします:
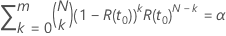
 信頼水準は次の式を満たします:
信頼水準は次の式を満たします:
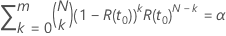
ある時点で、 、解は、
、解は、 の式は次の形式を取ります:
の式は次の形式を取ります:
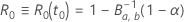
 、解は、
、解は、 の式は次の形式を取ります:
の式は次の形式を取ります:
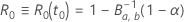
ここで、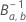 は、次の形状パラメータを持つベータ分布の逆累積分布関数です。
は、次の形状パラメータを持つベータ分布の逆累積分布関数です。
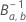 は、次の形状パラメータを持つベータ分布の逆累積分布関数です。
は、次の形状パラメータを持つベータ分布の逆累積分布関数です。
を計算するには、 、関数を逆数にします。
、関数を逆数にします。 .逆数は、分布全体によって異なります。
.逆数は、分布全体によって異なります。
 、関数を逆数にします。
、関数を逆数にします。 .逆数は、分布全体によって異なります。
.逆数は、分布全体によって異なります。
- 対数-位置-尺度全体

- 位置-尺度全体
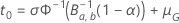
試験に合格する確率は、に依存する次の形式を取ります および改善:
および改善:
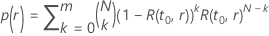
 および改善:
および改善:
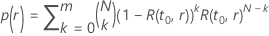
ここで、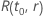 は、に関する分布モデルの信頼性関数です。
は、に関する分布モデルの信頼性関数です。 および
および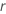 .
.
信頼性関数は、分布全体によって異なります:
- 対数-位置-尺度全体

- 位置-尺度全体
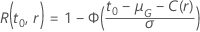
次の表は、関数を示しています。 分布族のと試験の目的:
分布族のと試験の目的:
| 信頼性の到達点 | ||||
|---|---|---|---|---|
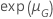
|

|
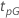
|

|
|
| 対数-位置-尺度 |  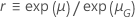 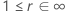 |
 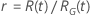  |
 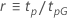 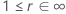 |
  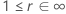 |
| 信頼性の到達点 | ||||
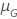
|

|
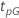
|

|
|
| 位置-尺度 | 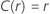  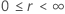 |
 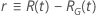  |
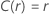  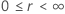 |
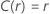 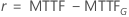 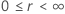 |
ここで、
の例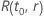 ワイブル分布の
ワイブル分布の
ワイブル分布の試験計画で、の信頼性の到達点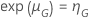 、与えられたサンプルサイズ、合格する確率は次の形式を取ります:
、与えられたサンプルサイズ、合格する確率は次の形式を取ります:
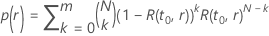
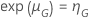 、与えられたサンプルサイズ、合格する確率は次の形式を取ります:
、与えられたサンプルサイズ、合格する確率は次の形式を取ります:
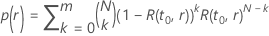
ここで

試験時間
実証試験の規格に試験時間が含まれている場合、合格する確率の計算にはサンプルサイズが必要です。与えられた試験時間で、のサンプルサイズ 信頼水準は次の式を満たします:
信頼水準は次の式を満たします:

 信頼水準は次の式を満たします:
信頼水準は次の式を満たします:

0故障試験計画の場合( )、方程式の解、
)、方程式の解、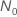 は、次の形式を取ります:
は、次の形式を取ります:

 )、方程式の解、
)、方程式の解、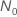 は、次の形式を取ります:
は、次の形式を取ります:

ここで

のとき、正確な解を数値で検索します .
.
試験に合格する確率は、に依存する次の形式を取ります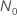 および改善:
および改善:
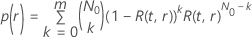
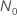 および改善:
および改善:
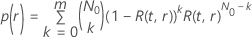
ここで、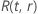 は、に関する分布モデルの信頼性関数です。
は、に関する分布モデルの信頼性関数です。 および
および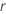 .
.
信頼性関数は、分布全体によって異なります:
- 対数-位置-尺度全体

- 位置-尺度全体
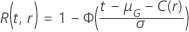
関数 は、試験の規格がサンプルサイズを与えるときと同じ定義を持ちます。
は、試験の規格がサンプルサイズを与えるときと同じ定義を持ちます。
の例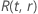 ワイブル分布の
ワイブル分布の
ワイブル分布の試験計画で、の信頼性の到達点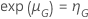 、与えられた試験時間、合格する確率は次の形式を取ります:
、与えられた試験時間、合格する確率は次の形式を取ります:
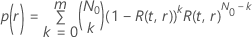
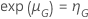 、与えられた試験時間、合格する確率は次の形式を取ります:
、与えられた試験時間、合格する確率は次の形式を取ります:
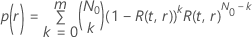
ここで

表記
| 用語 | 説明 |
|---|---|
| N | 試験の規格がサンプルサイズを提供する場合の、計画のサンプルサイズ |
| m | テスト中に故障するユニットの数 |
 | 有意水準(実証試験の信頼水準が |
 | 尺度パラメータ |
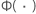 | 選択した対数-位置-尺度または位置-尺度分布の標準分布の累積分布関数 |
 | 選択した対数-位置-尺度または位置-尺度分布の標準分布の逆累積分布関数 |
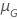 | 試験の目的を満たす分布の位置パラメータ |
 | ワイブル分布の形状パラメータ |
 | 試験の規格がサンプルサイズを提供する場合の試験時間 |
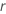 | 対数-位置-尺度規模分布の改善比または位置-尺度分布の改善量 |
 | 試験の目的である、時間tでの信頼度 |
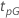 | 試験の目的である、パーセントpでの百分位数 |
 | 試験の目的である、故障までの平均時間 |
 | 試験の規格が試験時間を提供する場合の試験時間 |
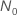 | 試験の規格が試験時間を提供する場合のサンプルサイズ |
1 W. Q. Meeker and L. A. Escobar (1998).
Statistical Methods for Reliability Data. Wiley, New
York.