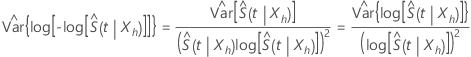生存関数
生存関数は、次の定義を使用します。
| 用語 | 説明 |
|---|---|
 | 明確な、順序付けされた、イベントの時間 |
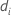 | 時間 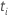 でのイベントの数 でのイベントの数 |
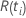 | 一定の時に設定されたリスク 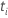 は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。 は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。
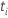 |
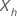 | 新規または既存のデータポイントを表す共変量値の p成分ベクトル |
与えられた 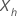 に、Cox比例ハザードモデルの生存関数は、次の形式で表されます。
に、Cox比例ハザードモデルの生存関数は、次の形式で表されます。
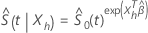
ここで、

および

関数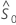 すべての共変量の値が 0 の場合、個人の生存関数が推定されます。関数
すべての共変量の値が 0 の場合、個人の生存関数が推定されます。関数 は、ベースライン累積ハザード率のブレスローの推定値です。関数
は、ベースライン累積ハザード率のブレスローの推定値です。関数 は、観測されたイベント時間にジャンプするステップ関数です。
は、観測されたイベント時間にジャンプするステップ関数です。
信頼区間
穏やかな規則性条件下で、推定器 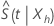 平均を持つ漸近正規分布を有する
平均を持つ漸近正規分布を有する  および漸近分散と以下の形式:
および漸近分散と以下の形式:
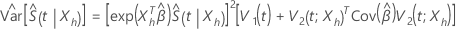
ここで、

および
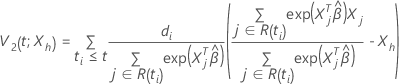
直接 Wald メソッドの信頼区間は利用できますが、分布が原因で精度が低くなります。 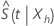 はひどく歪んでいます。また、このような区間の信頼限界は、しばしば間隔[0, 1]の外にあります。の対数の分布
はひどく歪んでいます。また、このような区間の信頼限界は、しばしば間隔[0, 1]の外にあります。の対数の分布 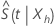 歪度が低く、正規分布に対してより速く収束します。Minitabでは、次の変換を使用して信頼区間を計算します。
歪度が低く、正規分布に対してより速く収束します。Minitabでは、次の変換を使用して信頼区間を計算します。
ログ変換
Minitabは の信頼区間を計算します 信頼限界を逆変換して、信頼区間を提供します。
信頼限界を逆変換して、信頼区間を提供します。 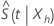 .このアプローチを使用すると、約
100(1 –
α) の信頼区間
.このアプローチを使用すると、約
100(1 –
α) の信頼区間 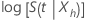 は、次の形式を取ります:
は、次の形式を取ります:
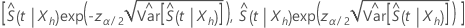
ここで、 の漸近分散を推定する
の漸近分散を推定する  は、次の形式を取ります:
は、次の形式を取ります:
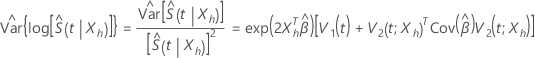
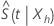 の信頼上限の場合
1 を超えると、上限として 1 が使用されます。
の信頼上限の場合
1 を超えると、上限として 1 が使用されます。
自然対数変換
ログ ログ変換により、信頼区間が 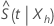 は区間(0、1)にありますMinitabでは両分布の信頼区間を計算します。
は区間(0、1)にありますMinitabでは両分布の信頼区間を計算します。 信頼限界を逆変換して、信頼区間を提供します。
信頼限界を逆変換して、信頼区間を提供します。 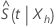 .この方法を使用すると、約
100(1 –
α) の信頼区間
.この方法を使用すると、約
100(1 –
α) の信頼区間  は、次の形式を取ります:
は、次の形式を取ります:
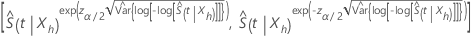
ここで、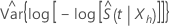 の漸近分散を推定する
の漸近分散を推定する  は、次の形式を取ります:
は、次の形式を取ります: