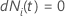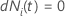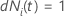| 用語 | 説明 |
|---|---|
 | 明確な、順序付けされた、イベントの時間 |
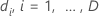 | 時間
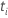 でのイベントの数 でのイベントの数 |
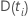 | イベントを発生するすべてのユニットのセット 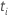 |
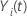 | 被験者
i が時間
t でリスクがある場合は値 1 を持つ標識変数、それ以外の場合は 0 に相当する標識変数 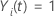 もしも もしも
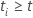 および および
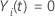 それ以外の場合 それ以外の場合
|
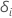 | 被写体
i が検閲されている場合の指標、 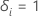 件名
が私は イベントを経験した場合、 件名
が私は イベントを経験した場合、 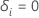 それ以外の場合 それ以外の場合 |
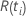 | 一定の時に設定されたリスク 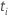 は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。
は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。 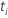 |
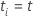
 | 時間 tまでの件名 i のイベントの数 |
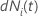 | の変更  件名
i に対しては、時間
が
件名
i に対しては、時間
が
|
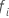 | 被験者 i がリスクセット内にある最初のイベント時刻 |
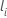 | 被験者 i がリスクセット内にある最後のイベント時刻 |
Cox-Snell残差
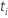 は、次の形式を取ります:
は、次の形式を取ります: 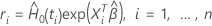
ここで、 は、ベースライン累積ハザード率のブレスローの推定値です。
は、ベースライン累積ハザード率のブレスローの推定値です。

 は、観測されたイベント時間でジャンプするステップ関数です。時間 でのジャンプのサイズ
は、観測されたイベント時間でジャンプするステップ関数です。時間 でのジャンプのサイズ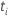 は、次の形式を取ります:
は、次の形式を取ります: 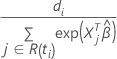

Efron近似の場合、Cox-Snell残差は次の形式になります。
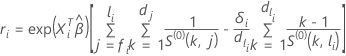
ここで、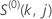 は、次の形式を取ります:
は、次の形式を取ります:
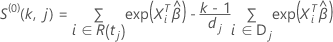
の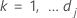
ここで、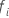 は、件名
i がリスクセット内にある最初のイベント時刻で、
は、件名
i がリスクセット内にある最初のイベント時刻で、 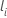 は、件名
i がリスク セット内にある最後のイベント時刻です。
は、件名
i がリスク セット内にある最後のイベント時刻です。
マーチンゲール残差

ここで、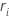 はコックススネル残差であり、タイの取り扱い方法に依存します。[加法]:
はコックススネル残差であり、タイの取り扱い方法に依存します。[加法]: 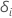 は、被写体
i が検閲されている場合の指標であり、次のような
は、被写体
i が検閲されている場合の指標であり、次のような 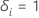 件名
が私は イベントを経験した場合、
件名
が私は イベントを経験した場合、 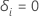 それ以外の場合
それ以外の場合
逸脱残差

ここで、 は、対象 i のマーチンゲール残差
です。
は、対象 i のマーチンゲール残差
です。
シェーンフェルト残差ベクトル
シェーンフェルト残差ベクトルは p成分ベクトルである。イベント時間 t の件名 i の場合、シェーンフェルト残差ベクトルは次の形式になります。
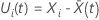
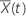 は、時間 t で設定されたリスクに対する共変量の加重平均です。加重平均は次の形式になります。
は、時間 t で設定されたリスクに対する共変量の加重平均です。加重平均は次の形式になります。 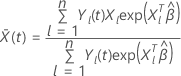
ここで、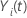 は
、被験者
i が時間
t でリスクがある場合は値 1 を持つ標識変数であり、それ以外の場合は 0 は、値 1 を持ちます。
は
、被験者
i が時間
t でリスクがある場合は値 1 を持つ標識変数であり、それ以外の場合は 0 は、値 1 を持ちます。 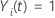 If
If
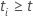 および
および
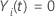 それ以外の場合
それ以外の場合
サブジェクトが時刻 tでイベントを経験しない場合、ベクターには欠損値が含まれます。
シェーンフェルト残差ベクトルの計算は、タイの取り扱い方法によって異なります。ブレスロー近似の場合、シェーンフェルト残差ベクトルは次の形式になります。
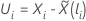
ここで、
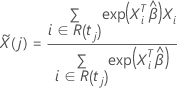
エフロン近似では、シェーンフェルト残差ベクトルは次の形式を持っています。
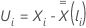
ここで、
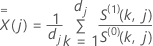
関数 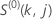 の定義は、単一規格限界のケースと同じです。
の定義は、単一規格限界のケースと同じです。
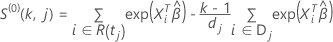
および
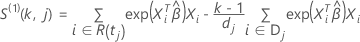
の
スケーリングされたシェーンフェルト残差ベクトル
スケーリングされたシェーンフェルト残差ベクトルは、次の形式で表されます。

ここで、 無修正生存時間の観測数であり、
無修正生存時間の観測数であり、 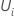 はシェーンフェルト残差ベクトルです。
はシェーンフェルト残差ベクトルです。
スコア残差ベクトル
スコア残差ベクトルの計算は、イベント時間における結び方の近似方法によって異なります。Breslow 近似では、スコア残差ベクトルは次の形式になります。
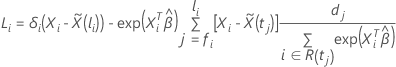
ここで、
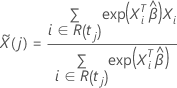
エフロン近似では、スコア残差ベクトルは次の形式になります。
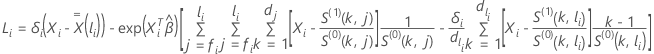
ここで、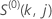 ,
,
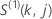 および
および  シェーンフェルト残差ベクトルと同じ定義を持つ:
シェーンフェルト残差ベクトルと同じ定義を持つ:
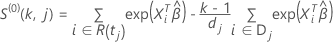
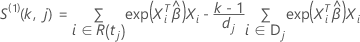
および
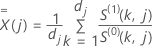
の
DFベータ
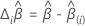

ここで、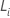 はスコア残差ベクトルです。しき
はスコア残差ベクトルです。しき い値の詳細は、,
を参照してください係数と回帰式の方法と式 固定予測変数のみでCoxモデルを適合 に移動.
い値の詳細は、,
を参照してください係数と回帰式の方法と式 固定予測変数のみでCoxモデルを適合 に移動.