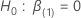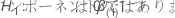分散分析は、モデル内の各予測変数の統計的有意性の検定を提供します。
自由度
オッズ比の解釈は、予測変数がカテゴリ変数か連続変数かによって変わります。カテゴリ予測変数の場合、自由度は予測変数(k – 1) の水準数 kより 1 より小さい値です。連続予測変数の場合、自由度は常に 1 です。上位の用語では、自由度は複合項の自由度の積です。たとえば、2 つの 3 レベルカテゴリ予測変数間の相互作用の自由度は、2 × 2 = 4 です。
カイ二乗
- ワルド検定
- 尤度比検定
- スコアテスト
クラスターが設計内に存在する場合、尤度比とスコア法ではクラスター内の観測値が独立していると仮定するため、Minitabは Wald 検定に基づいて ANOVA テーブルを提供します。
応答変数に関連付けられた応答時間がない場合、スコアテストは既知のログランクテストと同じです。
定義:
3 種類のテストの計算では、次の定義を使用します。
次のように定義します。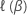 ブレスロー部分好感関数またはエフロン部分尤度関数 はβで評価されます。
ブレスロー部分好感関数またはエフロン部分尤度関数 はβで評価されます。
次のように定義します。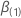 は
q-成分ベクトルと
は
q-成分ベクトルと 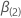 2 p成分係数ベクトルに以下の定義が含まれるように、a (p –
q)成分ベクトルである。
2 p成分係数ベクトルに以下の定義が含まれるように、a (p –
q)成分ベクトルである。  および
および 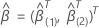 .
.
次のように定義します。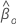 の
(部分的な) 可能性の最大値
の
(部分的な) 可能性の最大値  制限されたモデルの下で
制限されたモデルの下で
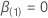 .次に、帰無仮説の下での最尤推定値は次の形式になります。
.次に、帰無仮説の下での最尤推定値は次の形式になります。
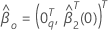
ここで、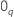 は
q-成分ベクトルで、ゼロと
は
q-成分ベクトルで、ゼロと  は
(部分的な) 可能性の最大値です
は
(部分的な) 可能性の最大値です 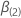 日時に変換
日時に変換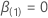 .
.
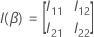
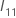 は
、q ×
q 行列です。
は
、q ×
q 行列です。 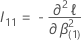
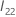 は 、p –
q ×
p –
q 行列です。
は 、p –
q ×
p –
q 行列です。 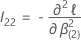
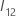 および
および  には、次の定義があります:
には、次の定義があります: 
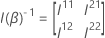
帰無仮説では、3つの検定(Wald、尤度比、およびスコア検定)の検定統計量は 、自由度q の漸近カイ二乗分布を持っています。漸近分布は、モデル内のパラメータの数と比較して、観測されたイベントの数が多い場合に有効です。カテゴリ予測変数の場合、各レベルのイベント数も十分に大きくなければなりません。
ワルド検定
Wald 検定の場合、検定統計量は次の形式になります。
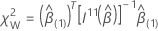
ここで、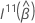 は
、q の上位
×のサブ 行列です。
は
、q の上位
×のサブ 行列です。  .
.
設計にクラスターがある場合、計算では Lin & Wei (1989)1.
次のように定義します。 はスコア残差の行列です。分散共分散行列には以下の形式があります。
はスコア残差の行列です。分散共分散行列には以下の形式があります。

ここで、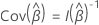 および
および  は、折りたたまれたスコア残差行列です。折りたたまれたスコア残差行列を取得するには、スコア残余行の各クラスターを残余行の合計で置き換えます。
は、折りたたまれたスコア残差行列です。折りたたまれたスコア残差行列を取得するには、スコア残余行の各クラスターを残余行の合計で置き換えます。
尤度比検定
尤度比検定での仮説は次のとおりです。
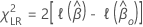
ここで、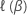 は、適切なモデルの部分対数尤度関数です。
は、適切なモデルの部分対数尤度関数です。
クラスターが設計内に存在する場合、尤度比とスコア法ではクラスター内の観測値が独立していると仮定するため、Minitabは Wald 検定に基づいて ANOVA テーブルを提供します。
スコアテスト
次のように定義します。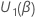 対数尤度関数の部分誘導体のベクトルである。
対数尤度関数の部分誘導体のベクトルである。
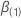 .具体的には、この
q-コンポーネント ベクトルは、次の形式を持っています。
.具体的には、この
q-コンポーネント ベクトルは、次の形式を持っています。
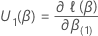
その後、スコア検定の検定統計量は次の形式になります。
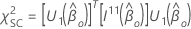
クラスターが設計内に存在する場合、尤度比とスコア法ではクラスター内の観測値が独立していると仮定するため、Minitabは Wald 検定に基づいて ANOVA テーブルを提供します。
p値
調整済みp値は次式を持ちます。
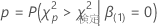
ここで、 は、カイ二乗分布に続くランダム変数です。
は、カイ二乗分布に続くランダム変数です。  の自由度。
の自由度。
 は検定統計量です。
は検定統計量です。