このトピックの内容
ステップ1:データに対するモデルの適合度を判断します
- p値 ≤ α:モデルは、データに適切に適合しています。
- p値が有意水準以下の場合、モデル間に統計的に有意な差があると結論付けることができます。いずれかの項が統計的に有意であるかどうかを調べ、また、モデルが比例ハザードの仮定を満たしていることを確認する必要があります。
- p値 > α:効果は統計的に有意であると結論付けるのに十分な証拠はありません。
- p値が有意水準より大きい場合は、条件が異なることによって応答が変化すると結論付けることはできません。項を持たないモデルを再適合したいと考えるかもしれません。
適合度検定
| 検定 | 自由度 | カイ二乗 | p値 |
|---|---|---|---|
| 尤度比 | 4 | 18.31 | 0.001 |
| ワルド(Wald) | 4 | 21.15 | 0.000 |
| スコア | 4 | 24.78 | 0.000 |
主要な結果: p値
これらの結果では、3 つのテストの p 値はすべて 0.05 未満であるため、モデルがデータに適合すると結論付けることができます。
ステップ 2: モデルにおける応答と項の間の関係が統計的に有意かどうか判断する
- p値 ≤ α:関連性は統計的に有意である
- p値が有意水準以下の場合は、応答変数と項の間に統計的に有意な関連性が存在すると結論付けることができます。
- p値 > α:その関連性は統計的に有意ではない
- p値が有意水準より大きい場合は、応答変数と項の間に統計的に有意な関連性があると結論することはできません。項を持たないモデルを再適合したいと考えるかもしれません。
- 変量因子が有意な場合は、その因子が応答の変動量に寄与していると結論できます。
- 共変量が統計的に有意な場合、その共変量の値の変化は平均応答値の変化と関連すると結論付けることができます。
- 交互作用項の係数が有意な場合は、因子と応答の間の関係はその項の他の因子に依存します。こうしたケースでは、交互作用の影響の考慮なしに主効果を解釈すべきではありません。
- 多項式項が有意な場合は、データに曲面性が含まれると結論付けることができます。
分散分析
| ワルド検定 | |||
|---|---|---|---|
| 要因 | 自由度 | カイ二乗 | p値 |
| 年齢 | 1 | 1.78 | 0.182 |
| ステージ | 3 | 17.92 | 0.000 |
主要な結果: p値
これらの結果では、ステージのp値は0.05のαレベルで有意です。したがって、癌の段階は、患者の生存に統計的に有意な影響を有すると結論付けることができる。ただし、年齢のp値は0.182であるため、年齢の影響は0.05のαレベルでは有意ではありません。
ステップ3:予測変数の相対的なリスクを決定する
- カテゴリ変数
-
カテゴリ予測変数の相対リスク表では、カテゴリ変数の2つのレベルがレベルAとレベルBにラベル付けされます。相対リスクは、レベル B に対するレベル A のイベント発生率を表します。例えば、次の結果では、ステージIVの患者に対する事象を経験するリスクは、ステージIの患者に対するリスクよりも5.5倍高い。
- 連続変数
- 連続予測変数の相対リスク表には、変化の単位と相対的リスクが表示されます。相対リスクは、予測変数値の 1 単位ごとのハザード率の変化を表します。例えば、次の結果では、患者は年齢に対して1年の増加ごとに事象を経験する可能性が1.02倍高い。
信頼区間を使用して、相対リスクが統計的に有意であるかどうかを判断できます。通常、信頼区間に 1 が含まれている場合、相対的リスクが統計的に有意であると結論付けることはできません。
連続予測変数の相対的リスク
| 変更ユニット | 相対的リスク | 95%信頼区間 | |
|---|---|---|---|
| 年齢 | 1 | 1.0192 | (0.9911, 1.0481) |
カテゴリ予測変数の相対的リスク
| 水準A | 水準B | 相対的リスク | 95%信頼区間 |
|---|---|---|---|
| ステージ | |||
| II | I | 1.1503 | (0.4647, 2.8477) |
| III | I | 1.9010 | (0.9459, 3.8204) |
| IV | I | 5.5068 | (2.4086, 12.5901) |
| III | II | 1.6526 | (0.6819, 4.0049) |
| IV | II | 4.7872 | (1.7825, 12.8566) |
| IV | III | 2.8968 | (1.2952, 6.4788) |
主要な結果: 相対リスク、95% CI
ステップ4:モデルが比例ハザードの仮定を満たすかどうかを判断する
- 比例ハザード表の検定
-
検定を使用して、モデルが比例ハザードの仮定を満たしているかどうかを判断します。帰無仮説は、モデルがすべての予測変数の仮定を満たしていることです。通常、0.05の有意水準(αまたはアルファとも呼ばれる)が有効に機能します。0.05の有意水準は、実際にはモデルによって応答の変動は説明できないにも関わらず、説明できると結論付ける可能性が5%であることを示しています。
p値が有意水準以下の場合、データは分布に従わないと結論付けることができます。p値が有意水準より大きい場合、そのモデルにより応答での変動が説明されると結論することはできません。
- アルハスプロット
-
Arjas プロットを使用して、モデルがカテゴリ予測変数の比例ハザード仮定を満たしているかどうかを判断します。プロット上の曲線が 45 度線と異なる場合、モデルは予測変数の比例ハザード仮定を満たしていません。
モデルが変数の仮定を満たしていない場合は、代わりに階層化変数として変数を使用してみてください。
- アンデルセンプロット
-
異なる地層に対する比例ハザードの仮定をモデルが満たしているかどうかを判断するには、アンダーセンプロットを使用します。1 つ以上の階層化変数の値のそれぞれの組み合わせによって、階層が定義されます。プロットには、各階層の曲線が含まれています。モデルが仮定を満たしている場合、曲線は X = 0 および Y = 0 の点を通る直線になります。地層のベースラインハザードレートがX軸上の地層のベースラインハザードレートと同じ場合、曲線はプロット上の45度基準線に従います。
モデルが仮定を満たしていない場合は、モデルが比例ハザードの仮定を満たしていない階層変数でデータを分割するかどうかを検討します。次に、データの各サブセットに対して個別の分析を実行します。個別の分析は、各サブセットの予測変数に異なる効果をもたらします。
比例ハザードの検定
| 項 | 自由度 | 相関 | カイ二乗 | p値 |
|---|---|---|---|---|
| 年齢 | 1 | 0.1328 | 1.18 | 0.278 |
| ステージ | ||||
| II | 1 | -0.0104 | 0.01 | 0.940 |
| III | 1 | -0.2445 | 2.86 | 0.091 |
| IV | 1 | -0.1193 | 0.63 | 0.426 |
| 全体 | 4 | — | 4.61 | 0.330 |
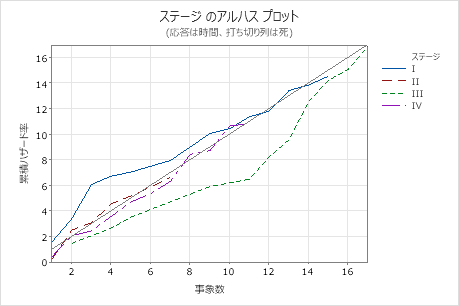
主要な結果: P値、アルハスプロット
これらの結果では、比例ハザードの検定のp値はすべて0.05より大きいので、モデルが比例ハザードの仮定を満たしていないと結論付けることはできません。
Arjas プロットには、累積ハザード率と、 の各レベルのイベント数の比較が表示されます ステージ。この Arjas プロットでは、一般的に線は 45 度の線に従うので、モデルは予測変数の比例ハザードの仮定を満たしていると結論付けることができます ステージ。
