Minitab統計ソフトウェアにおける比例ハザード仮定のテストでは、グランブシュとテノー(1994)1.
自由度
自由度は、推定係数ごとに 1 です。全体の検定では、自由度は係数の自由度の合計です。
カイ二乗
全予測変数のグローバルテスト
この検定では、モデル内のすべての項の傾きが、スケールされたシェーンフェルト残差と、少なくとも 1 つの傾きがゼロではないという対立仮説に対するイベント時間の時間スケール変換との関係に対してゼロであるという帰無仮説を評価します。
モデル内のすべての予測変数の同時検定の検定統計量は、次の形式で示されます。

比例ハザードの仮定がすべての予測変数に当てはまるという帰無仮説の下で、  は、p 自由度のカイ2乗分布を漸近的に追跡します。
は、p 自由度のカイ2乗分布を漸近的に追跡します。
個々の予測変数の検定
検定では、1 つの項のスケールされたシェーンフェルト残差と、傾斜がゼロではないという対立仮説に対するイベント時間の時間スケール変換との関係について、傾きがゼロであるという帰無仮説を評価します。
個々の予測変数に関する検定統計量は、次の形式で示されます。
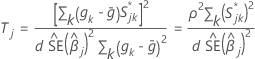
プロポーショナルハザードの仮定が予測変数に対して真であるという帰無仮説の下で、 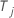 は、1自由度のカイ2乗分布を漸近的に追跡します。
は、1自由度のカイ2乗分布を漸近的に追跡します。
表記
| 用語 | 説明 |
|---|---|
 | イベント時間 |
| d | イベントの回数 |
| p | モデル内の項の数 |
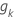 | イベント時間のタイムスケール変換。Minitab Statistical SoftwareのT管理図
|
 | 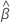 の分散共分散行列 の分散共分散行列 |
| S | シェーンフェルト残 差の d×p 行列 |
| S | スケールされたシェーン フェルト残差の d×p 行列 |
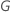 | の中心値を成分とする
d次元ベクトル 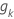 どこ
どこ  |
 |  |
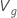 | の成分の標本分散 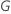 |
 | の成分のサンプル平均 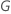 |
 | ベクトルの
j番目 の成分の標準誤差 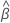 Cox比例ハザードモデルからの推定パラメータの
Cox比例ハザードモデルからの推定パラメータの |
 | j番目 の予測変数のスケーリングされたシェーンフェルト残差と時間変換された関数値との間の相関係数
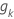 |
p値
検定のp値 

ここで、 は、カイ二乗分布に続くランダム変数です。
は、カイ二乗分布に続くランダム変数です。  自由度。
自由度。
 は検定統計量です。
は検定統計量です。
1 Grambsch, P.M. and
Therneau, T.M.からのアプローチを使用しています。(1994).Proportional hazards tests and
diagnostics based on weighted residuals.
Biometrika 81(3), 515-526.
