使用する方法また計算式を選択します。
このトピックの内容
要約統計の場合は、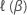 
は、β で評価されたBreslow部分尤度関数またはEfron部分尤度関数です。関数は、分析の仕様に依存します。項のないモデルの計算では、
を使用します 
.項を含むモデルの計算では、
を使用します 
どこ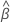 
は(部分的な)最大尤度推定値です。 
.
対数尤度
| 用語なし | 用語付き |
|---|---|
 |
 |
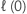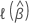R二乗
R2 統計量は、項を持つモデルに対してのみ存在します。Minitab統計ソフトウェアは、Nagelkerke(1991)1.
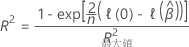
ここで、
はサンプルサイズで、
は、次の形式を取ります： 
はサンプルサイズで、
は、次の形式を取ります： R2の式では、分子はコックス & スネル一般化 R2 統計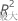 
は、その統計の最大許容値です。
AIC、AICc、BIC
用語なし
項を使用しない場合、異なる情報基準の式は次の等価性に低下します。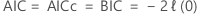 
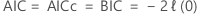
用語付き
打ち切られた生存モデルの場合、Minitab統計ソフトウェアは、観測された事象の数をサンプルサイズとして情報基準を計算します。「ヴォリンシー&ラフティ(2000)2
この調整に関する情報を参照してください。用語では、情報基準には次の式が含まれます。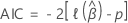 
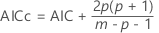
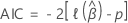
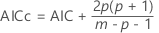
ここで、
は、フォレスト内の木の数と
は、観測されたイベントの数です。
1 Nagelkerke,
N.J.D.で提案コックス&スネル一般化R2 の標準化版を計算します。(1991).A note on the general
definition of the coefficient of determination.
Biometrika, 78(3), 691-692.
https://doi.org/10.1093/biomet/78.3.691
2 Volinsky,
C.T. & Raftery, A.E.(2000). Bayesian information criterion for censored
survival models.Biometrics 56(1), 256-262.
https://doi.org/10.1111/j.0006-341X.2000.00256.x
