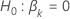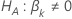回帰式
半パラメトリック Cox 比例ハザード モデルでは、個人の予測変数値を使用します。 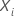 、リスクスコアを予測するために、
、リスクスコアを予測するために、
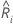 .回帰式は、次の一般形式を取ります。
.回帰式は、次の一般形式を取ります。

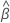 は、推定された係数のベクトルです。推定係数には、連続予測変数の平方など、より高い順序の項の値を含めることができます。推定リスクスコアは、調査の全期間に有効であり、時間に依存しません。出力では、方程式は、カテゴリ因子の異なるレベルに対して別々の式が現れる次の形式を持ちます。
は、推定された係数のベクトルです。推定係数には、連続予測変数の平方など、より高い順序の項の値を含めることができます。推定リスクスコアは、調査の全期間に有効であり、時間に依存しません。出力では、方程式は、カテゴリ因子の異なるレベルに対して別々の式が現れる次の形式を持ちます。
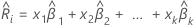
係数
Cox比例ハザードモデルの対数部分尤度関数を 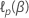 .部分尤度関数
を最大化するベクトル
.部分尤度関数
を最大化するベクトル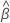 は、モデルの推定係数を示します。見つけます
は、モデルの推定係数を示します。見つけます 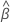 、対数偏数尤度関数の部分微分をゼロに設定し、次の式を解く
、対数偏数尤度関数の部分微分をゼロに設定し、次の式を解く
 .Minitab統計ソフトウェアは、ニュートン・ラフソン反復法を使用して方程式を解きます。マレー(1972)1 ニュートン・ラフソン反復法の説明については、
.Minitab統計ソフトウェアは、ニュートン・ラフソン反復法を使用して方程式を解きます。マレー(1972)1 ニュートン・ラフソン反復法の説明については、
対数部分尤度関数の部分誘導体のベクトルは、応答変数に結合イベント時間が含まれているかどうかによって異なります。応答変数にタイが含まれる場合、推定では Efron 近似または Breslow 近似法が使用されます。応答変数に結びがない場合、3 つのメソッドすべてが同じ推定値を提供します。データ内のタイが少ないほど、2 つの近似メソッドの結果が近くなります。データ内のタイが多いほど、ブレスロー近似値が改善されます。
| 用語 | 説明 |
|---|---|
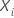 | イベント時間を持つサンプル単位に対応する共変量値のベクトル 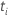 |
結びつきのないデータ
| 用語 | 説明 |
|---|---|
 | イベントの回数 |
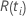 | 一定の時に設定されたリスク 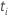 は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。
は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。 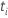 |
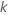 | モデル内のパラメーター数のカウント変数、 ここで ここで
 は、モデル内のパラメーターの数です。
は、モデル内のパラメーターの数です。 |
関係のない Cox 比例ハザード モデルの部分尤度関数は、次の形式になります。
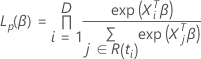
損失関数は次の形を取ります。
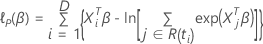
 は、次の形式を取ります:
は、次の形式を取ります:
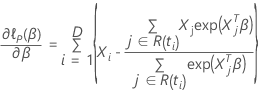
特定の係数の部分導関数が、 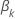 は、次の形式を取ります:
は、次の形式を取ります:
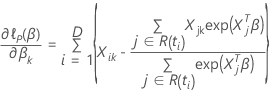
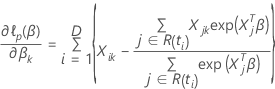
結びつきのあるデータ
| 用語 | 説明 |
|---|---|
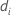 | 時間 でのイベントの数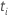 |
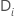 | イベントを一度に持つすべてのサンプルユニットのセット 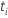 |
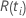 | 一定の時に設定されたリスク 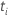 は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。
は、時間の前にまだ故障していないすべてのサンプルユニットのセットです。 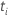 |

データの結びつきに対するエフロン近似
損失関数は次の形を取ります。
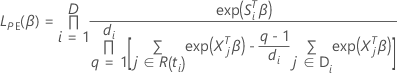
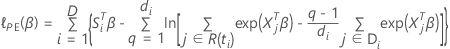
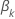 は、次の形式を取ります:
は、次の形式を取ります: 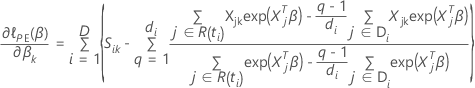
結びつきのあるデータのブレスロー近似
損失関数は次の形を取ります。
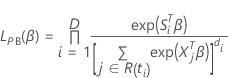
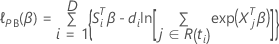
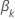 は、次の形式を取ります:
は、次の形式を取ります: 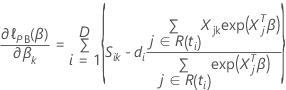
コード化係数
この表には、分析によって連続予測変数が標準化される際に、コード化された係数が表示されます。コード化された係数を見つけるには、標準化された予測変数を上記の式に代入します。
係数の標準誤差(SE Coef)
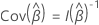
観測された情報行列、  応答変数に、タイ付きイベント時間が含まれているかどうかによって異なります。応答変数にタイが含まれる場合、推定では Efron 近似または Breslow
近似法が使用されます。応答変数に結びがない場合、3 つのメソッドすべてが同じ推定値を提供します。データ内のタイが少ないほど、2
つの近似メソッドの結果が近くなります。データ内のタイが多いほど、ブレスロー近似値が改善されます。
応答変数に、タイ付きイベント時間が含まれているかどうかによって異なります。応答変数にタイが含まれる場合、推定では Efron 近似または Breslow
近似法が使用されます。応答変数に結びがない場合、3 つのメソッドすべてが同じ推定値を提供します。データ内のタイが少ないほど、2
つの近似メソッドの結果が近くなります。データ内のタイが多いほど、ブレスロー近似値が改善されます。
結びつきのないデータ
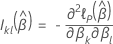
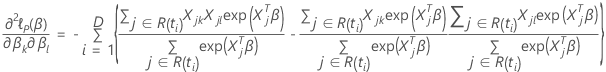
データの結びつきに対するエフロン近似
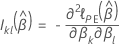
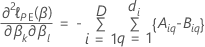
ここで、
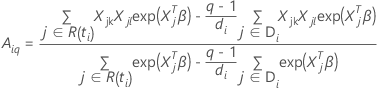
および
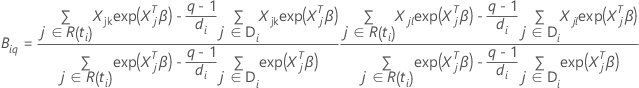
結びつきのあるデータのブレスロー近似
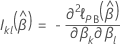
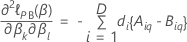
ここで、
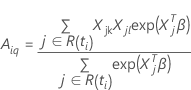
および
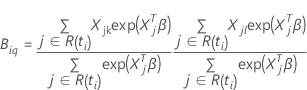
Z値
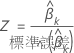
ここで、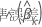 は、の推定標準誤差です
は、の推定標準誤差です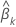 。係数
.の値
。係数
.の値 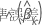 は
、k番目 の対角要素の正の平方根です。
は
、k番目 の対角要素の正の平方根です。  .
.
信頼率
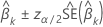
ここで、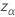 は、標準正規分布の上限
α パーセンタイルポイントです。
は、標準正規分布の上限
α パーセンタイルポイントです。
p値

| 用語 | 説明 |
|---|---|
 | 標準正規分布のランダム変数 |
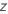 | の検定統計量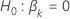 と対立仮説 と対立仮説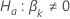 |
階層化比例ハザードモデル
s レベルを 成層変数として含むカテゴリ変数を含むモデルの場合、回帰係数は階層全体で一定です。階層化モデルの回帰係数の推定は、階層化のない比例ハザードモデルと同じプロセスを持ちます。階層化モデルの場合、対数部分尤度関数の形式は次のとおりです。

ここで、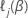 は、ストラタム j 内の対数の部分的尤度
です。各層全体の微分を合計して、部分尤度方程式を得る。各地層の微分は、階層化のない比例ハザードモデルの微分と同じです。ブレスロー法とエフロン法は、それに応じて適用されます。
は、ストラタム j 内の対数の部分的尤度
です。各層全体の微分を合計して、部分尤度方程式を得る。各地層の微分は、階層化のない比例ハザードモデルの微分と同じです。ブレスロー法とエフロン法は、それに応じて適用されます。