ある品質エンジニアが、電子装置内のトランジスタ間の漏電を調査したいと考えています。漏電が特定のしきい値に達すると電子装置は故障します。試験での故障を加速させるため、装置は通常よりも大幅に高い温度で試験されました。装置は、故障がないかどうか2日ごとに点検されました。
エンジニアは、通常動作条件(55° C)と最悪事例動作条件(85° C)で装置が故障するまでの時間を推定するために加速寿命試験を実行します。エンジニアは、B5寿命を調べたいと考えています。これは、装置の5%が故障するまでの経過時間の推定量です。
- サンプルデータを開く、漏電.MWX.
- を選択します。
- 応答は打ち切られていない/任意打ち切りデータを選択します。
- 変数/開始変数に、開始日を入力します。
- 終了変数に、終了日を入力します。
- 度数列に、故障数を入力します。
- 加速変数に、温度を入力します。
- 関係から、Arrheniusを選択します。
- 仮定する分布から、ワイブルを選択します。
- 推定をクリックします。百分位数と確率推定で、新しい予測変数を入力するを選択して、新しい温度を入力します。
- 次のパーセントに対する百分位数を推定するに5を入力し、OKをクリックします。
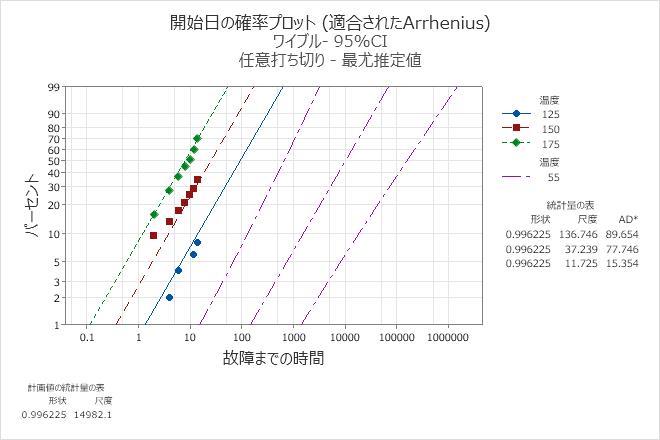
- グラフをクリックします。プロットに含める計画値に、55と入力します。
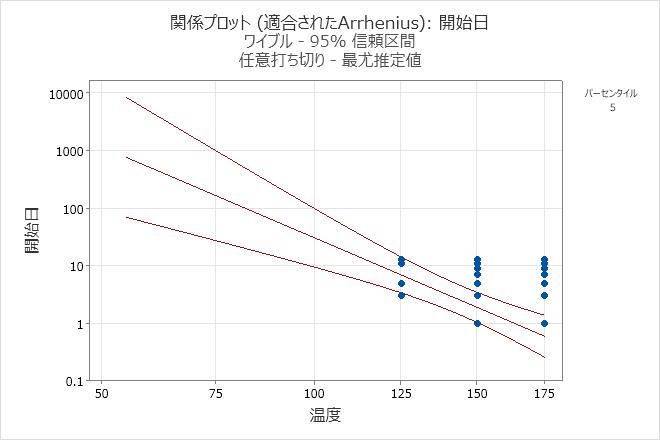
- 関係プロットで、次のパーセントに対する百分位数をプロットするに5と入力して、故障時間をプロットに表示するを選択します。
- 各ダイアログボックスでOKをクリックします。
結果を解釈する
百分位数表の結果に基づいて、エンジニアは次の結論を出すことができます。
- 設計温度(55℃)では、装置の5%が約760日(約2年)後に故障します。
- 最悪事例の温度(85℃)では、装置の5%が約81日後に故障します。
適合されたモデルに基づく確率プロットは、加速変数の各水準における分布、変換、および同等の形状(ワイブル分布)の仮定が適切かどうかを判断するのに役立ちます。これらのデータでは、点はほぼ直線に従います。したがって、モデルの仮定は加速変数水準に対して適切です。
応答変数の開始:開始日 終了: 終了日
度数: 故障数
打ち切り
| 打ち切り情報 | 計数 |
|---|---|
| 右打ち切り値 | 95 |
| 区間打ち切り値 | 58 |
推定法:最尤法
分布: ワイブル
加速変数との関係: Arrhenius
回帰表
| 95.0%正規信頼区間 | ||||||
|---|---|---|---|---|---|---|
| 予測変数 | 係数 | 標準誤差 | z値 | p値 | 下限 | 上限 |
| 切片 | -17.0990 | 4.13633 | -4.13 | 0.000 | -25.2061 | -8.99195 |
| 温度 | 0.755405 | 0.157076 | 4.81 | 0.000 | 0.447542 | 1.06327 |
| 形状 | 0.996225 | 0.136187 | 0.762071 | 1.30232 | ||
対数尤度 = -191.130
パーセンタイル表
| 95.0%正規信頼区間 | |||||
|---|---|---|---|---|---|
| パーセント | 温度 | パーセンタイル | 標準誤差 | 下限 | 上限 |
| 5 | 55 | 759.882 | 928.717 | 69.2500 | 8338.21 |
| 5 | 85 | 81.0926 | 63.2317 | 17.5897 | 373.855 |