このトピックの内容
係数とは
係数は、式内の変数に掛ける数値です。たとえば、y = -3.6 + 5.0X1 - 1.8X2という式では、変数X1とX2をそれぞれ5.0と-1.8に掛けるので、5.0と-1.8が係数になります。
式内の係数のサイズおよび符号は、グラフに影響を与えます。単純な一次方程式(1つの変数xのみが含まれる)では、係数は線の傾きになります。
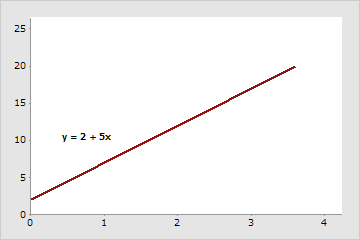
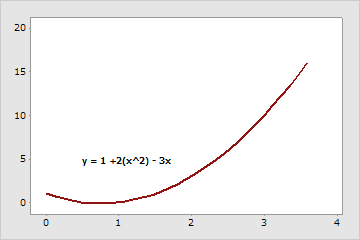
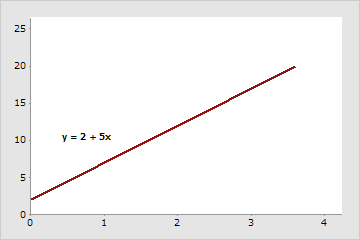
係数(および傾き)は正の値5です。

係数は、2と-3です。
回帰式を計算してデータをモデル化すると、サンプルに基づいて各予測変数の係数が推定され、係数表に表示されます。たとえば、次の回帰式の出力では、次の係数表が表示されます。
回帰式
熱流量 = 325.4 + 2.55 東 + 3.80 南 - 22.95 北 + 0.0675 対日照量 + 2.42 時刻
この式では、焦点の位置、対日照量、および時刻に基づいて熱流束を予測します。この式の係数値は2番目の列に表示されます。
係数
係数の標
項 係数 準誤差 t値 p値 VIF
定数 325.4 96.1 3.39 0.003
東 2.55 1.25 2.04 0.053 1.36
南 3.80 1.46 2.60 0.016 3.18
北 -22.95 2.70 -8.49 0.000 2.61
対日照量 0.0675 0.0290 2.33 0.029 2.32
時刻 2.42 1.81 1.34 0.194 5.37
各係数は、X以外の予測変数がすべて一定の場合に、Xが1単位分増加したときの平均応答の変化量を予測します。たとえば回帰式で、変数「北」が1単位分増加して他の変数は変化しない場合、熱流量は平均で約22.95単位減少します。
係数のp値が、選択された有意水準(0.05など)よりも小さい場合、予測変数と応答の関係は統計的に有意になります。また、Minitabでは、式の定数の値が係数列に示されます。
注
係数という用語は、指標(相関係数、決定係数、またはケンドルの係数など)として使用される計算された数値を表すのに使用されることもあります。
回帰係数の信頼区間を計算する
信頼区間を使用すると、係数のパラメータの信頼性を評価できます。信頼区間が広くなるほど、推定値の精度は下がります。
- を選択します。
- ダイアログボックスに入力します。
- 結果をクリックします。
- 結果の表示から拡張表を選択します。各ダイアログボックスでOKをクリックします。
注
デフォルトでは、両側95%信頼区間が計算されます。デフォルト設定を変更するには、を選択し、オプションをクリックします。信頼水準と区間のタイプを指定します。
