2つの事象のオッズを比較するにはオッズ比を使用します。オッズ比とは、特定の条件が存在する場合の成功のオッズ(見込み)を異なる条件が存在する場合の成功のオッズで割ったものです。たとえば、学校に登校せずに自宅学習した生徒のグループと学校教育を受けた生徒のグループを比較したいとします。この分析の目的は、どちらのグループが大学を優等成績で卒業する見込みが高いかどうかを判断することです。オッズ比は次のように計算されます。
- 自宅学習
-

- 学校教育
-

- オッズ比
-
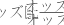
分母の水準は参照レベルと呼ばれています。この例では、「学校教育」が参照レベルです。オッズ比が3.0に等しい場合、優等成績で卒業するオッズ比は、自宅学習の生徒が学校教育を受けた生徒の3倍になります。
logitリンク関数を選択することで、オッズ比を使用できます。ロジスティック回帰のオッズ比では、カテゴリ応答変数の各水準の見込みを比較します。オッズ比は、各予測変数が各応答水準の確率にどのように影響するかを数値化します。たとえば、ハイブリッドカーを選択するのに顧客の年齢と性別が影響するかどうかを判断したいとします。次の変数を含むロジスティック回帰モデルを作成します。
| 変数 | 種類 | 説明 |
|---|---|---|
| ハイブリッド | 2値応答変数 | 顧客がハイブリッドカーを購入しなかったら0、購入したら1。 |
| 性別 | 2値予測変数 | 顧客が男性なら0、女性なら1。参照水準は男性です。 |
| 年齢 | 連続予測変数 | 顧客の年齢と等しいです。任意の非負数値と等しくなります。 |
ロジスティック回帰手順により両方の予測変数が有意であると宣言されていると仮定します。「性別」のオッズ比が2.0の場合、ハイブリッドカーを購入する女性のオッズ比は男性のオッズ比の2倍になります。「年齢」のオッズ比が1.05の場合、年齢が1年追加されるたびに顧客がハイブリッドカーを購入するオッズ比は5%増加します。
