係数の最尤推定値の収束を妨げる状況として、完全分離と準完全分離の2つがあります。
完全分離
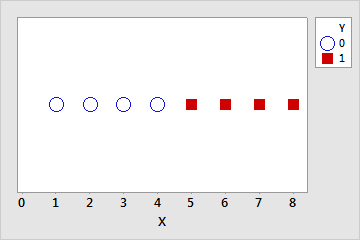
完全分離は、予測変数の線形の組み合わせによって応答変数の完全な予測が実現する場合に起こります。たとえば、次のデータセットでX ≤ 4の場合はY = 0です。X > 4の場合はY = 1です。
| Y | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |
準完全分離
準完全分離は完全分離に似ています。予測変数はほとんどの予測変数について応答変数の完全な予測を実現しますが、すべてではありません。たとえば、前のデータセットでX = 4の値の1つでYが0ではなく1であるとします。この場合、X < 4の場合はY = 0、X > 4の場合はY = 1ですが、X = 4の場合はYは0または1になります。このデータの中間域における重なりにより、分離が準完全になります。
| Y | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 |
| X | 1 | 2 | 3 | 4 | 4 | 4 | 5 | 6 | 7 | 8 |

原因と修正
多くの場合、低確率の事象を観測するのにデータセットが小さすぎる場合に分離が発生します。モデルに含まれる予測変数が多いほど、データ内の個別グループのサンプルサイズが小さくなるため、分離が発生する可能性が高くなります。
分離が検出されると警告が表示されますが、モデルに含まれる予測変数が多いほど、分離の原因の特定が難しくなります。モデルに交互作用項が含まれる場合、原因の特定がさらに難しくなります。
分離が原因で最尤推定値の収束に失敗した場合は、次の5つの方法を検討してください。
- データの量を増やす。多くの場合、応答の1つの値のみが含まれる予測変数のカテゴリまたは範囲がある場合に分離が発生します。サンプルサイズが大きいほど、応答に異なる値が含まれる確率が高くなります。
- 分離が示唆する内容を検討します。完全分離と準完全分離はサンプルサイズが小さすぎることを示す可能性がありますが、重要な関係を示す可能性もあります。特定の水準または水準の組み合わせでの事象の真の確率が0または1に近い場合、この情報が重要になります。
- 代替モデルを検討します。モデルに項が多くなるほど、少なくとも1つの変数で分離が発生する確率は高くなります。モデルの項を選択すると、項を除外することにより最尤推定値は収束できます。項を使用していない有用なモデルがある場合、新しいモデルを使用して分析を継続できます。
- 問題のある変数のカテゴリを組み合わせることができるかどうかを確認する。組み合わせに適した複数のカテゴリが存在する場合、データセットから分離を排除できる可能性があります。たとえば、「果物」がモデル内の変数であるとします。試行回数が少ないため、「グレープフルーツ」には事象がありません。「グレープフルーツ」と「オレンジ」をカテゴリ「かんきつ類」に組み合わせることで、分離が排除されます。
表 1. 完全分離のあるデータ 果物 事象 試行 グレープフルーツ 0 10 オレンジ 5 100 りんご 25 100 バナナ 40 100 表 2. 重なりのあるデータ 果物 事象 試行 かんきつ類 5 110 りんご 25 100 バナナ 40 100 - 問題のあるカテゴリ変数が集約変数であるかどうかを確認する。応答に対する非集約変数の関係で完全分離が示されない場合、数値データを置換することで分離が排除される可能性があります。たとえば、「雇用期間」がモデル内の集約変数であるとします。データが30日ごとに増分する場合、最低水準にすべての事象が含まれ、最高水準には事象が含まれないため、完全分離が発生します。モデル内の日数を置換することで、分離が排除されます。
表 3. 完全分離のあるデータ 長さのカテゴリ 事象 試行 1–90 2 2 91–180 1 2 181–270 1 2 271–360 0 2 正確な長さ 事象 試行 45 1 1 60 1 1 95 1 1 176 0 1 185 0 1 241 1 1 280 0 1 299 0 1
参考文献
分離に関する詳細は、Albert、J. A. Anderson(1984年)「On the existence of maximum likelihood estimates in logistic regression models」『Biometrika』71巻1号、1~10ページ
