2値ロジスティック回帰には、2値応答・度数フォーマットと事象・試行フォーマットの2つの異なるフォーマットにデータを入力できます。出力の一部の統計量の信頼性と解釈は、データフォーマットによって変わります。各データフォーマットを使用するタイミングについては、2値ロジスティック回帰で各データフォーマットを使用する場合を参照してください。
逸脱度R2および調整済み逸脱度R2の解釈に対するデータフォーマットの効果
2値ロジスティック回帰では、データフォーマットは、逸脱度R2および調整済み逸脱度R2の値を解釈する方法に影響を与えます。事象・試行フォーマットでは、観測された各観測値は、そのデータ行のすべての試行の事象の確率を表します。通常、この確率は試行数が多いときのためであり、0~1の値を取ります。対照的に、2値応答・度数フォーマットの各観測値は、通常1回のみの試行を表します。1回の試行で観測される値は1か0のいずれかです。
一般に、データフォーマットの差によって、データの総逸脱度は変わります。事象・試行データでは、逸脱度は、予測された確率と観測された確率の差異と関係があります。2値応答・度数フォーマットでは、逸脱度は予測された確率と試行ごとの0%または100%の結果との差異に関係します。逸脱度R2および調整済み逸脱度R2は、通常、事象・試行フォーマットのデータでは高くなります。
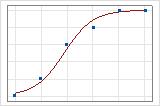
グラフの例では差がはっきりとわかります。これらのプロットでは、記号はデータの観測値を表し、曲線はモデルの予測値を表します。事象・試行データでは、記号はラインの近くに分布します。事象・試行データの逸脱度R2の値は約96%です。モデルは平均確率を非常に良好に予測します。
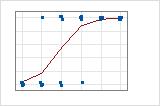
2値応答・度数データでは、観測値は、線が0%または100%に近似するときのみ予測線に近似します。2値応答・度数データの逸脱度R2の値は約56%です。予測確率と個々のケースとの関係はそれほど強くありません。
2値応答・度数データで逸脱度の適合度検定が誤解を招きやすい理由
2値ロジスティック回帰では、データフォーマットは、逸脱度の適合度検定の信頼性に影響を与えます。通常、逸脱度の適合度検定のp値は行ごとの試行数が減るにつれて小さくなります。2値応答・度数フォーマットデータの行ごとの試行回数は、通常ほとんどありません。このため、適合が適切な場合でも、データが2値応答・度数フォーマットにある場合は、低い適合度を示す可能性があります。逸脱度の適合度検定は、データが事象・試行フォーマットでも行ごとの試行回数が少ない場合は、誤って低い適合度を示す可能性もあります。
ホスマー-レメショウ検定は、データのフォーマットに左右されません。データの各行の試行回数がほとんどない場合、ホスマー-レメショウ検定は、データに対するモデルの適合度を示す指標として、信頼度が高まります。
異なるフォーマットのデータが同じ場合、これら2つの結果を比較します。これらのデータでは、モデルの形式は適切です。応答の情報、係数、ホスマー-レメショウ検定の結果は同じです。逸脱度の適合度検定の結果は、データフォーマットによって変わります。
これらの結果では、データは、度数列のない2値応答・度数フォーマットになっています。分析では500行のデータを使用します。各行が1つの試行を表しています。0.05の有意水準では、逸脱度の適合度検定のp値はモデルの適合度が低いことを示しています。このp値により、モデルのフォーマットが適切でないことがわかります。2値応答・度数フォーマットでデータを収集する場合、逸脱度の適合度検定は信頼できないことが多くなります。
2値ロジスティック回帰:Y 対 X
これらの結果では、データは事象・試行フォーマットになっています。分析では5行のデータを使用します。行ごとのデータは、100回の試行回数を表します。0.05の有意水準では、逸脱度の適合度検定のp値はモデルの適合度が低いという根拠は見つかりません。事象・試行フォーマットでデータを収集する場合、通常、逸脱度の適合度検定は信頼できます。
2値ロジスティック回帰:事象 対 X
2値応答・度数データでピアソンの適合度検定が誤解を招きやすい理由
2値ロジスティック回帰では、データフォーマットは、ピアソン適合度検定の信頼性に影響を与えます。ピアソン検定で使用する近似カイ二乗分布は、データに含まれる行ごとの事象の期待数が小さい場合は不正確になります。2値応答・度数フォーマットのデータには、通常、行ごとの試行回数はほとんどありません。それゆえ、データのフォーマットが2値応答・度数の場合のピアソンの適合度検定は不正確になる可能性があります。
ホスマー-レメショウ検定は、データのフォーマットに左右されません。データの各行の試行回数がほとんどない場合、ホスマー-レメショウ検定は、データに対するモデルの適合度を示す指標として、信頼度が高まります。
異なるフォーマットでデータが同じ場合、これら2つの結果を比較します。これらのデータでは、モデルの形式は適切ではありません。真のモデルには、X1とX2の交互作用が含まれます。応答の情報、係数、ホスマー-レメショウ検定の結果は同じです。ピアソン適合度検定の結果は、データフォーマットによって変わります。
これらの結果では、データは、度数列のある2値応答・度数フォーマットデータになっています。分析では18行のデータを使用します。行ごとのデータは、250回のベルヌイ試行を表します。0.05の有意水準では、ピアソンの適合度検定のp値は、モデルが適合していることを示します。このp値により、モデルが適切であるという結論が正しくないことがわかります。2値応答・度数フォーマットでデータを収集する場合、ピアソンの適合度検定は通常は信頼できません。
2値ロジスティック回帰:Y 対 X1, X2
これらの結果では、データは事象・試行フォーマットになっています。分析では9行のデータを使用します。行ごとのデータは、500回の試行回数を表します。0.05の有意水準では、ピアソンの適合度検定のp値は、モデルがデータに適合していないことを示します。事象・試行フォーマットでデータを収集する場合、ピアソンの適合度検定は、通常は信頼できます。
