このトピックの内容
回帰分析とは
回帰分析では、1つの式を生成して、1つ以上の予測変数と応答変数の間の統計的関係を説明し、新しい観測値を予測します。線形回帰では一般に、二乗残差の合計を最小限にすることによって式を導出する通常の最小二乗推定法を使用します。
たとえば、ポテトチップ会社に勤務していて、発送前に砕けたポテトチップのコンテナあたりの割合に影響する因子(応答変数)を分析するとします。2つの予測変数として、他の原料に対する相対的なポテトの割合と調理温度(摂氏)を含めて、回帰分析を実施します。以下が結果表です。
データを設定する
- 調理温度が摂氏1℃上昇するごとに、砕けるチップの割合は0.022%増すと予期されます。
- ポテト0.5(50%)、調理温度175℃の設定で砕けるチップの割合を予測するには、砕けるポテトチップ7.7%(4.251 - 0.909 * 0.5 + 0.2231 * 175 = 7.70075.)の予測値を計算します。
- 各係数の符号は、関係の方向を示します。
- 係数は、モデル内の他の予測変数を一定に保ちながら、予測変数での1つの変更単位について、応答における平均変化を表します。
- 各係数のp値により、係数がゼロに等しい(効果なし)かどうか帰無仮説を検定します。したがって、p値が低い場合は、対象のモデルに追加されたその予測変数は有意であることを示します。
- この式は、指定された予測変数の値が与えられることにより新しい観測値を予測します。
注
1つの予測変数を持つモデルは単回帰と呼ばれます。複数の予測変数を持つモデルは重回帰と呼ばれます。
単回帰とは
単回帰では、2つの連続変数、すなわち1つの応答変数(Y)と1つの予測変数(X)の線形関係を調べます。2つの変数が関連している場合、偶然性より高い確度で予測変数から応答値を予測することができます。
- 予測変数が変化するにつれ、応答変数がどのように変化するかを調べます。
- 任意の予測変数(X)に対し、応答変数の値(Y)を予測します。
重回帰とは
重回帰では、1つの連続応答と2つ以上の予測変数との間の線形関係を調べます。
予測変数が多数ある場合は、回帰モデルをすべての予測変数に適合する前に、ステップワイズ法またはベストサブセットによるモデル選択手法を使うことにより、予測変数をスクリーニングして応答と関係のない予測変数を排除します。
通常の最小二乗回帰とは
最小二乗(OLS)回帰では、サンプルのデータ点と方程式から推定される値との距離の平方和が最小となる方程式を求めることで推定式が計算されます。
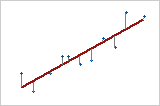
応答対 予測変数
予測変数が1つ(単回帰)の場合は、各データ点と回帰直線間の平方距離の和をできるだけ小さくします。
最小二乗回帰に対して満たす必要がある前提
- 回帰モデルがその係数で線形になっています。最小二乗は、(係数ではなく)変数を変換することで曲線としてモデル化できます。任意の曲線をモデル化するために、適切な関数形式を指定する必要があります。
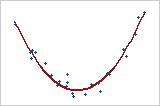
2次モデル
ここで、予測変数Xは曲線をモデル化するために二乗されています。Y = bo + b1X + b2X2
- 残差の平均値が0です。モデルに定数を含めると、平均値が強制的に0になります。
- すべての予測変数が残差と相関していません。
- 残差が互いに相関していません(連続相関)。
- 残差に均一な分散が存在します。
- どの予測変数も別の予測変数と完全な相関関係(r=1)にありません。不自然に高い相関(多重共線性)も避けることをお勧めします。
- 残差が正規分布に従います。
最小二乗回帰では、これらの前提がすべて満たされたときにだけ最良の予測ができるため、これらを検定しておくことは大切です。一般的な検定方法としては、残差プロットを調べる、不適合検定を実施する、分散拡大係数(VIF)を使って予測変数間の相関を調べることなどがあります。
