傾きは直線の勾配を示し、切片は軸との交差位置を示します。傾きと切片により2つの変数間の線形関係を定義し、平均変化率を推定するために使用できます。傾きが大きくなるほど線が急勾配になり、変化率が大きくなります。
直線の方程式を調べることにより、傾きとy切片(線とY軸との交差点)をすばやく見つけられます。
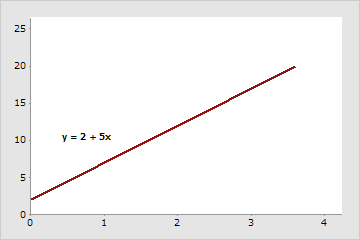
傾きは5です。xが1増加すると、yは5増加します。yの切片は2です。
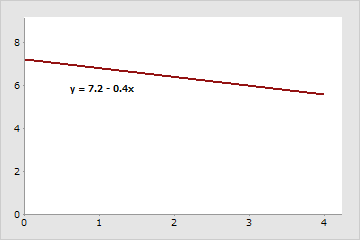
傾きは-0.4です。xが1増加すると、yは0.4減少します。y切片は7.2です。

傾きは0です。xが1増加しても、yは増減しません。y切片は-4です。
通常、この関係はy = b0 + b1xという方程式で表すことができます。b0はy切片を表し、b1は傾きを表します。
たとえばある会社が、生産部門で働く従業員の業務遂行能力をy = 130 + 4.3x という回帰モデルを使用して予測できると判断したとします。ここで、xは従業員が受ける社内教育の時間(0~20)を表し、yは職業技能検定での従業員のスコアを表します。y切片の値(130)は、社内教育を受けていない従業員の平均職業技能スコアを示しています。傾きの値(4.3)は、社内教育の時間が増えるごとに、職業技能スコアが平均で4.3ポイント増加することを示しています。
