平均応答法と下側のみの規格限界を持つモデルの保存期間
時間、バッチ、および時間*バッチの交互作用を持つモデル
バッチ効果とバッチ*時間交互作用がモデルにある場合、xij時間におけるi番目のバッチの適合値では以下のモデルを使用します。
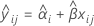
保存期間を確認するには、以下の式を下側規格限界と等しくなるように設定し、時間(x)を解きます。

ここで
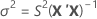
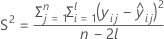
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するには、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が下側規格限界よりも統計的に大きいかを判断します。
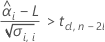
次に、時系列に対して、平均応答が統計的に有意な割合で減少するかどうかを判断します。

最初の応答が非常に高く、時間が経つにつれて応答が減少する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
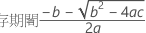
ここで
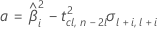

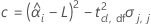
時間とバッチを持つモデル
バッチ*時間交互作用がモデルにない場合、傾きはすべてのバッチで同じです。時間xijにおけるi番目のバッチの適合値では以下のモデルを使用します。
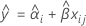
保存期間を確認するには、以下の式を下側規格限界と等しくなるように設定し、時間(x)を解きます。

ここで

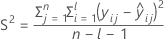
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するには、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が下側規格限界よりも統計的に大きいかを判断します。
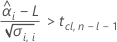
次に、時系列に対して、平均応答が統計的に有意な割合で減少するかどうかを判断します。
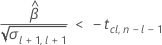
最初の応答が非常に高く、時間が経つにつれて応答が減少する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
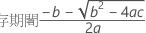
ここで



時間を持つモデル
時間しかモデルにない場合、傾きと切片はすべてのバッチで同じです。時間xijにおける適合値では以下のモデルを使用します。
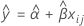
保存期間を確認するには、以下の式を下側規格限界と等しくなるように設定し、時間(x)を解きます。

ここで
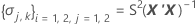
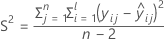
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するため、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が下側規格限界よりも大きいかを判断します。
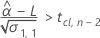
次に、時系列に対して、平均応答が減少するかどうかを判断します。
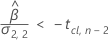
最初の応答が非常に高く、時間が経つにつれて応答が減少する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
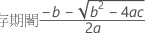
ここで
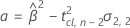


表記
| 用語 | 説明 |
|---|---|
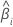 | i番目のバッチの傾き |
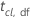 | 信頼水準(cl)のt統計量と自由度(df) |
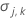 | 推定されたパラメータベクトルの分散 |
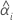 | i番目のバッチの切片 |
| L | 下側規格限界 |
| X | 計画行列 |
| i | 保存期間推定値があるバッチを表示するインデックス |
| l | バッチ因子の水準の数 |
| yij | i番目のバッチの応答値とj番目の時間 |
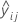 | i番目のバッチの適合値とj番目の時間 |
| n | 応答値の総数 |
平均応答法と上側のみの規格限界を持つモデルの保存期間
時間、バッチ、および時間*バッチの交互作用を持つモデル
バッチ効果とバッチ*時間交互作用がモデルにある場合、xij時間におけるi番目のバッチの適合値では以下のモデルを使用します。
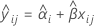
保存期間を確認するには、以下の式を上側規格限界と等しくなるように設定し、時間(x)を解きます。
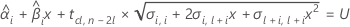
ここで
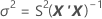
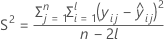
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するには、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が統計的に上側規格限界未満であるかを判断します。
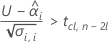
次に、時系列に対して、平均応答が統計的に有意な割合で増加するかどうかを判断します。
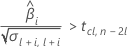
最初の応答が十分に低く、時間が経つにつれて応答が増加する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
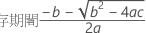
ここで
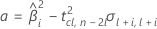
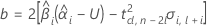
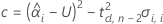
時間とバッチを持つモデル
バッチ*時間交互作用がモデルにない場合、傾きはすべてのバッチで同じです。時間xijにおけるi番目のバッチの適合値では以下のモデルを使用します。
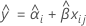
保存期間を確認するには、以下の式を上側規格限界と等しくなるように設定し、時間(x)を解きます。

ここで

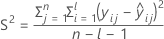
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するには、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が統計的に上側規格限界未満であるかを判断します。
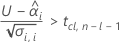
次に、時系列に対して、平均応答が統計的に有意な割合で増加するかどうかを判断します。
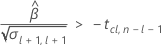
最初の応答が十分に低く、時間が経つにつれて応答が増加する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
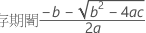
ここで



時間を持つモデル
時間しかモデルにない場合、傾きと切片はすべてのバッチで同じです。時間xijにおける適合値では以下のモデルを使用します。
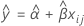
保存期間を確認するには、以下の式を上側規格限界と等しくなるように設定し、時間(x)を解きます。

ここで
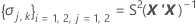
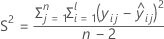
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
有意な保存期間を計算するため、Minitabは2つの条件を評価します。まず、時間 = 0のときに平均応答が上側規格限界未満であるかを判断します。
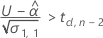
次に、時系列に対して、平均応答が増加するかどうかを判断します。
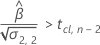
最初の応答が十分に低く、時間が経つにつれて応答が増加する場合、Minitabは保存期間を計算します。保存期間を計算するには、以下の2次式を使用します。
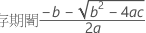
ここで
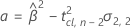

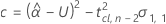
表記
| 用語 | 説明 |
|---|---|
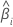 | i番目のバッチの傾き |
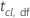 | 信頼水準(cl)のt統計量と自由度(df) |
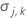 | 推定されたパラメータベクトルの分散 |
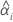 | i番目のバッチの切片 |
| U | 上側規格限界 |
| X | 計画行列 |
| i | 保存期間推定値があるバッチを表示するインデックス |
| l | バッチ因子の水準の数 |
| yij | i番目のバッチの応答値とj番目の時間 |
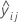 | i番目のバッチの適合値とj番目の時間 |
| n | 応答値の総数 |
両方の限界
時間、バッチ、時間*バッチの交互作用を持つモデル
2つの条件を評価して、保存期間に有意な推定値があるかを判断します。まず、平均応答が統計的に規格限界の範囲内にあるかを判断します。
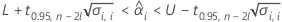
ここで
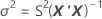
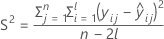
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
次に、時系列に対して、平均応答が統計的に有意な割合で変化するかどうかを判断します。
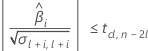
有意な推定値がある場合、Minitabでは、時間が経つにつれて平均応答が増加または減少するかが判断されます。2番目の条件が偽の場合、以下の条件の1つが真になります。
時間が経つにつれて応答は減少します。

時間が経つにつれて応答は増加します。
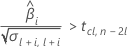
時系列に対して応答平均が減少する場合、Minitabは、下側規格限界に関連する保存期間を計算します。増加する場合、Minitabは上側規格限界に関連する保存期間を計算します。
時間とバッチを持つモデル
2つの条件を評価して、保存期間に有意な推定値があるかを判断します。まず、平均応答が統計的に規格限界の範囲内にあるかを判断します。
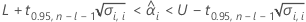
ここで

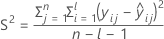
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
次に、時系列に対して、平均応答が統計的に有意な割合で変化するかどうかを判断します。
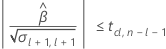
有意な推定値がある場合、Minitabでは、時間が経つにつれて平均応答が増加または減少するかが判断されます。2番目の条件が偽の場合、以下の条件の1つは真になります。
時間が経つにつれて応答は減少します。
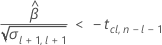
時間が経つにつれて応答は増加します。
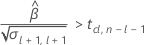
時系列に対して応答平均が減少する場合、Minitabは、下側規格限界に関連する保存期間を計算します。増加する場合、Minitabは上側規格限界に関連する保存期間を計算します。
時間を持つモデル
2つの条件を評価して、保存期間に有意な推定値があるかを判断します。まず、平均応答が統計的に規格限界の範囲内にあるかを判断します。
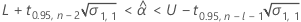
ここで
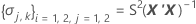
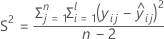
I = バッチ水準の総数
n = 応答値の総数
X = モデルの計画行列
次に、時系列に対して、平均応答が統計的に有意な割合で変化するかどうかを判断します。
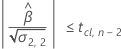
有意な推定値がある場合、Minitabでは、時間が経つにつれて平均応答が増加または減少するかが判断されます。2番目の条件が偽の場合、以下の条件の1つは真になります。
時間が経つにつれて応答は減少します。
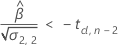
時間が経つにつれて応答は増加します。
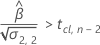
時系列に対して応答平均が減少する場合、Minitabは、下側規格限界に関連する保存期間を計算します。増加する場合、Minitabは上側規格限界に関連する保存期間を計算します。
表記
| 用語 | 説明 |
|---|---|
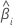 | i番目のバッチの傾き |
| l | バッチ因子の水準の数 |
| n | データの行数 |
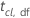 | df(自由度)を持つt分布から得られるclにおける逆累積分布関数の値 |
