変量バッチの安定性分析の方法

混合モデルの一般形

混合効果モデルには、固定効果とランダム効果の両方が含まれます。混合モデルの一般形は以下になります。

y = Xβ + Z₁μ₁+ Z₂μ₂ + ... + Z_cμ_c + ε

表記

混合モデルの特殊形

安定性分析は、変量バッチ因子と共に2つのモデルを適合します。最大モデルには、時間、変量バッチ因子、時間とバッチの間のランダム交互作用が含まれます。

y = Xβ + Z₁μ₁+ Z₂μ₂ + ε

小さいモデルには、時間、変量バッチ因子が含まれます。

y = Xβ + Z₁μ₁+ε

応答ベクトルyの一般的な分散共分散行列は以下になります。

V(σ²) = V(σ², σ²₁, ... , σ²_c) = σ²I_n + σ²₁Z₁Z'₁ + ... + σ²_cZ_cZ'_c

ここで

σ² = (σ², σ²₁, ... , σ²_c)'

σ², σ²₁, ... , σ²_cは分散成分と呼ばれます。

分散から因数分解することで、混合モデルの対数尤度の計算部分にあるH(θ)の表現を見つけることができます。

V(σ²) = σ²H(θ) = σ²[I_n + θ₁Z₁Z'₁ + ... + θ_cZ_cZ'_c]

バッチが変量因子の場合、未知のパラメータ推定値は、制限された対数尤度関数の負の値を2倍したものを最小化することで発生します。最小化は、制限された対数尤度関数の最大化と同じです。最小化する関数は以下になります。

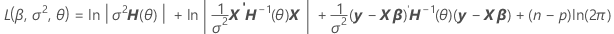
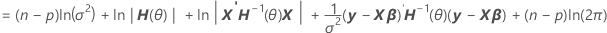
表記

ボックスｰコックス変換では、以下に示す通り、二乗値の残差合計を最小化するλ値が選択されます。出力される変換は、λ ≠ 0の場合にY^λ、およびλ = 0の場合にln(Y)です。λ < 0の場合に、変換済み応答に−1を掛けて、変換されていない応答の順序を維持します。

−2～2の範囲で最適値が検索されます。値がこの区間外になった場合、適合性が低下することがあります。

以下は一般的な変換方法です（Y′はデータYの変換データ）。

ラムダ（λ）値	変換
λ = 2	Y′ = Y 2
λ = 0.5	Y′ =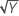
λ = 0	Y′ = ln(Y )
λ = −0.5
λ = −1	Y′ = −1 / Y

バッチ*時間の交互作用が有意な場合、分析は最初のモデルに適合します。この交互作用が有意ではないものの、2番目のモデルでバッチ項が有意な場合、分析は2番目のモデルに適合します。そうでない場合、分析は3番目のモデルに適合します。

バッチを併合するかどうかを判断する検定は、両方ともカイ二乗分布によって変動しますが、バッチが含まれている検定とは若干異なります。検定統計量の計算式とp値は以下のとおりです。

モデル1とモデル2の間の検定

差 = −2L₂ − (−2L₁)

p = 0.5 * Prob(χ²₁ > 差) + 0.5 * Prob(χ²₂ > 差)

モデル2とモデル3の間の検定

差 = −2L₃ − (−2L₂)

p = 0.5 * Prob(χ²₁ > 差)

表記

参考文献

1. Searle, S.R.、Casella, G.、McCuloch, C.E（1992）、Variance Components
2. West, B.T.、Welch, K.B.、Galecki, A.T.（2007）、Linear Mixed Models: A Practical Guide Using Statistical Software
3. Chow, S.（2007）、Statistical Design and Analysis of Stability Studies