使用する方法を選択します。
このトピックの内容
ボックスーコックス変換
ボックスーコックス変換では、以下に示す通り、二乗値の残差合計を最小化するλ値が選択されます。出力される変換は、λ ≠ 0の場合にYλ、およびλ = 0の場合にln(Y)です。λ < 0の場合に、変換済み応答に−1を掛けて、変換されていない応答の順序を維持します。
−2~2の範囲で最適値が検索されます。値がこの区間外になった場合、適合性が低下することがあります。
以下は一般的な変換方法です(Y′はデータYの変換データ)。
| ラムダ(λ)値 | 変換 |
|---|---|
| λ = 2 | Y′ = Y 2 |
| λ = 0.5 | Y′ = 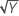 |
| λ = 0 | Y′ = ln(Y ) |
| λ = −0.5 |  |
| λ = −1 | Y′ = −1 / Y |
固定バッチのモデル選択
モデル選択は、保存期間がバッチによって変わるかどうか、時間の効果がバッチによって変わるかどうかを判断します。以下の3つのモデルが順番に検討されます。
- 時間 + バッチ + バッチ*時間(バッチごとに傾きと切片が異なる)
- 時間 + バッチ(傾きが等しく、切片がバッチごとに異なる)
- 時間(バッチ全体で傾きと切片が等しい)
バッチ*時間の交互作用が有意な場合、分析は最初のモデルに適合します。この交互作用が有意ではないものの、2番目のモデルでバッチの項が有意な場合、分析は2番目のモデルに適合します。そうでない場合は、分析は3番目のモデルに適合します。
検定統計量は以下になります。
モデル選択では、F分布を使用して、因子を検定します。F分布のパラメータは以下になります。
- 分子の自由度 = 項の自由度
- 分母の自由度 = 誤差の自由度
p値は、検定統計量よりも大きいF分布の比率です。


表記
| 用語 | 説明 |
|---|---|
| MS | 平均平方 |
| MSE | 誤差の平均平方 |
| F(x) | xにおいて評価される所定のF分布の累積分布関数 |
参考文献
1. Chow, S.(2007)、Statistical Design and Analysis of Stability Studies
2. アメリカ合衆国保健福祉省食品医薬品局(2004)、Guidance for Industry, Q1E Evaluation of Stability Data
