目的の方法または計算式を選択してください。
適合値
予測されたYまたは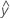
は、推定回帰式を使用して得られた予測変数値の平均応答値です。
周辺適合値の標準誤差（SE Fit）
混合モデルの周辺適合値の標準誤差は、固定効果の検定方法により異なります。どちらの方法でも、標準誤差は適合値の分散行列の対角要素の平方根です。
ケンワードｰロジャー法
ここで
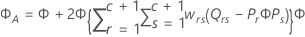
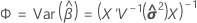
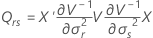
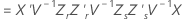
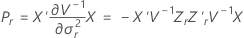
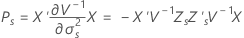
サタスウェイトの近似
ここで
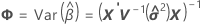
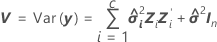
残差
残差は、観測値と適合値の差です。この部分の観測値は適合モデルでは説明されません。観測値の残差は以下になります。
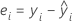
バッチが変量因子の場合、Minitabは2種類の残差を計算します。周辺残差では、変量バッチの適合値を使用するので、バッチの係数は式内にはありません。
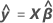
条件付き残差では、データにあるバッチの適合値を使用します。
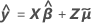
表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測応答値 |
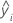 | i番目の適合応答値 |
 | 適合応答値のベクトル |
| X | 固定効果の計画行列 |
 | 固定予測変数のベクトル |
| Z | 変量因子の計画行列 |
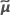 | 推定BLUP値のベクトル |
標準化残差
標準化残差は、「内部的スチューデント化残差」とも呼ばれます。
残差の標準偏差は、残差分散行列の適切な対角平方根です。
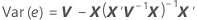
ここで
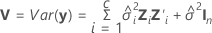
表記
| 用語 | 説明 |
|---|---|
| ei | i番目の残差 |
| Std(ei) | i番目の残差の標準偏差 |
信頼区間
特定の予測値における推定された平均応答値が分類されると予測される範囲。
混合モデルの適合値の標準誤差は、以下の行列の対角要素の平方根です。
ここで
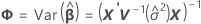
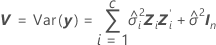
自由度は、バッチが変量因子の場合に以下の計算式を使用します。
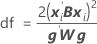
ここで
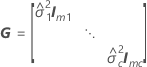
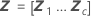
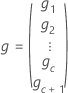
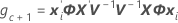
表記
| 用語 | 説明 |
|---|---|
| t1-α/2, df | 所定の自由度を持つt分布から得られる1–α/2百分位 |
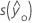 | 適合値の標準誤差 |
| X | 計画行列（定数を含む） |
| X' | Xの転置 |
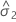 | 誤差の分散成分 |
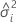 | i番目の変量因子の分散成分 |
| Zi | モデル内のi番目のランダム効果に対する既知のコーディングのn x mi行列 |
| Zi' | Ziの転置 |
| In | nの行と列を持つ恒等行列 |
| xi | 適合または予測の予測変数値 |
| W | 誤差の分散成分の漸近的な分散共分散行列 |
| c | モデル内のランダム効果の数 |
予測区間
新しい観測値の予測応答が含まれると予想される範囲。予測区間の計算は、周辺適合値または条件付き適合値の区間を計算するかどうかによって変わります。
周辺適合値
ここで
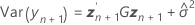
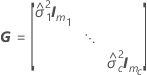
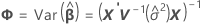
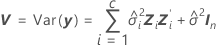
t統計量の自由度は以下の計算式で条件づけられます。
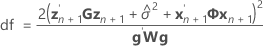
ここで
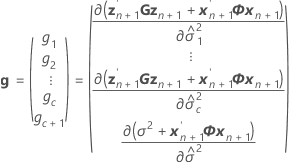
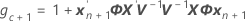
条件付き適合値
ここで
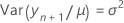
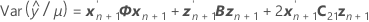
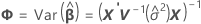
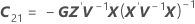
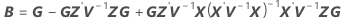
t統計量の自由度は以下になります。
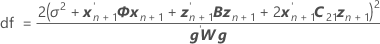
ここで
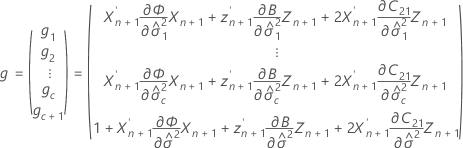
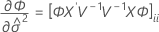
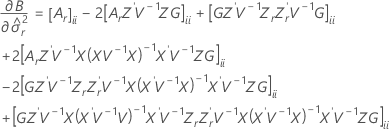
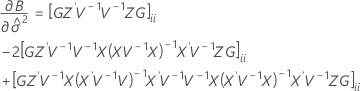
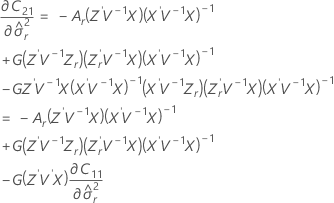
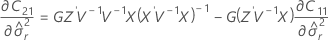
表記
| 用語 | 説明 |
|---|---|
 | 所定の自由度を持つt分布から得られる1–α/2百分位 |
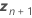 | ランダム予測変数の新しい値のベクトル |
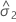 | 誤差の分散成分 |
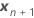 | 固定予測変数の新しい値のベクトル |
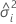 | i番目の変量因子の分散成分 |
| Im | mの行と列を持つ恒等行列 |
| m | モデル内のi番目のランダム項を表す計画行列の列数 |
| c | モデル内のランダム効果の数 |
| Zi | モデル内のi番目のランダム効果に対するn x mi計画行列 |
| Z'i | Ziの転置 |
