目的の方法または計算式を選択してください。
平方和(SS)
行列項において、異なる平方和の計算式は以下になります。



Minitabでは、逐次平方和と調整平方和の両方を使って回帰平方和の成分または処理平方和の成分を各項で説明される変動量に分解します。
表記
| 用語 | 説明 |
|---|---|
| b | 係数のベクトル |
| X | 計画行列 |
| Y | 応答値のベクトル |
| n | 観測値数 |
| J | 全て1のn×n行列 |
調整平均平方~回帰
回帰の平均平方(MS)を表す式は以下になります。

表記
| 用語 | 説明 |
|---|---|
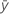 | 平均応答 |
 | i番目の適合された応答 |
| p | モデルにおける項の数 |
調整平均平方…誤差
平均平方誤差(略はMS ErrorまたはMSE、表記はs2)は適合回帰線からの分散です。式は以下になります。

表記
| 用語 | 説明 |
|---|---|
| yi | i番目の観測された応答値 |
 | i番目の適合された応答 |
| n | 観測値数 |
| p | 定数を含まないモデル内の係数の数 |
F
モデルに含まれる全ての因子が固定されている場合、F統計量の計算は、以下のように仮説検定手法により変わります。
- F(項)
-

- F(不適合度)
-

モデルに変量因子がある場合、Fは各項の平均平方の期待値情報を使って構築されます。詳細は、ニーターその他を参照してください。1
表記
| 用語 | 説明 |
|---|---|
| 調整平均平方項 | モデル内に含まれるその他の項を説明した後、項によってどれだけの変動を説明できるかを測定する測度です。 |
| 平均平方誤差 | モデルによって説明できない変動を測定する測度です。 |
| 平均平方不適合度 | モデルに項を追加することによってモデル化できる応答の変動を測定する測度です。 |
| 平均平方純粋誤差 | 反復応答データの変動を測定する測度です。 |
- J. Neter, W. Wasserman and M.H. Kutner (1985). Applied Linear Statistical Models, 第2版 Irwin, Inc.
p値(P)
p値は、仮説検定で帰無仮説を棄却できるかどうかを決定するために使用されます。p値は帰無仮説が真の場合に、実際の計算値と少なくとも同程度以上の極端な検定統計量が得られる確率です。p値用によく使用されるカットオフ値は0.05です。たとえば、検定統計量の計算されたp値が0.05未満の場合、帰無仮説を棄却します。
