ある製薬会社の品質エンジニアが、新しい薬品を含む錠剤の保存期間を特定したいと考えています。錠剤中の薬品の濃度は時間が経つにつれて減少します。エンジニアは、錠剤がいつ目的の濃度の90%に達するのかを特定したいと考えています。新しい薬品であるため、保存期間の推定に使用できる試験用のバッチは5つのみです。各バッチから1錠ずつの錠剤を9回の異なるタイミングで試験します。
保存期間を推定するため、エンジニアは安定性分析を行います。エンジニアはバッチのすべてをサンプリングしたため、バッチは変量因子ではなく固定因子です。
保存期間.MTW サンプルデータを開きます。応答 に薬品濃度 を入力します。時間 に月 を入力します。バッチ にバッチ を入力します。下側規格 に、90 と入力します。グラフ をクリックします。保存期間プロット の下の2番目のドロップダウンリストから、個別バッチのグラフなし を選択します。残差プロット で、一覧表示 を選択します。各ダイアログボックスのOK をクリックします。
結果を解釈する
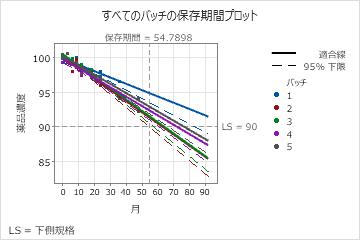
ICH（医薬品規制調和国際会議；International Conference on Harmonisation of Technical Requirements for Registration of Pharmaceuticals for Human Use）の2003年のガイドラインに従うには、エンジニアは、モデルに含める項にp値0.25を選択します。バッチ交互作用別の「月」のp値は0.048です。p値は有意水準0.25未満のため、エンジニアは、バッチごとの回帰式の傾きは異なりますと結論付けます。バッチ 3 には最も急な勾配 -0.1630 があり、これは、濃度がバッチ 3 で最も速く減少することを示します。バッチ 2 は最短の保存期間である 54.79 を持つため、全体の保存期間は Batch 2 の保存期間です。
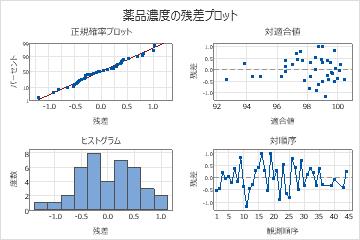
残差は正規に十分に近似しており、0付近にランダムに分布しています。残差対適合値プロットでは、右側よりも左側の方が点が少なくなっています。このパターンは、濃度が高い場合に品質エンジニアが研究の早期段階で収集するデータ量を増やしたため発生しました。このパターンは、分析の仮説を損なうものではありません。
モデル選択 (α = 0.25)
月 1 122.460 122.460 345.93 0.000 バッチ 4 2.587 0.647 1.83 0.150 月*バッチ 4 3.850 0.962 2.72 0.048 誤差 30 10.620 0.354 合計 39 139.516
モデル要約
0.594983 92.39% 90.10% 85.22%
係数
定数 100.085 0.143 701.82 0.000 月 -0.13633 0.00769 -17.74 0.000 1.07 バッチ 1 -0.232 0.292 -0.80 0.432 3.85 2 0.068 0.292 0.23 0.818 3.85 3 0.394 0.275 1.43 0.162 3.41 4 -0.317 0.292 -1.08 0.287 3.85 5 0.088 0.275 0.32 0.752 * 月*バッチ 1 0.0454 0.0164 2.76 0.010 4.52 2 -0.0241 0.0164 -1.47 0.152 4.52 3 -0.0267 0.0136 -1.96 0.060 3.65 4 0.0014 0.0164 0.08 0.935 4.52 5 0.0040 0.0136 0.30 0.769 *
回帰式
1 薬品濃度 = 99.853 - 0.0909 月 2 薬品濃度 = 100.153 - 0.1605 月 3 薬品濃度 = 100.479 - 0.1630 月 4 薬品濃度 = 99.769 - 0.1350 月 5 薬品濃度 = 100.173 - 0.1323 月
異常な観測値の適合値と診断
11 98.001 99.190 -1.189 -2.21 R 43 92.242 92.655 -0.413 -1.47 X 44 94.069 93.823 0.246 0.87 X
保存期間の推定
下側規格 = 90
1 83.552 2 54.790 3 57.492 4 60.898 5 66.854 全体 54.790
