ステップ1. モデルの成分数を判断する
PLSの目的は、適切な数の成分を持つモデルを選択することであり、それによって適正な予測が可能になります。PLSモデルを適合する場合、交差検証を実行して、モデル内の成分の最適数を決定するのに役立てることができます。Minitabでは、交差検証によって予測R2の値が最大のモデルが選択されます。交差検証を使用しない場合、モデルに含める成分数を指定またはデフォルトの成分数を使用することができます。デフォルトの成分数は、10、または、データ内の予測変数の数(いずれか少ない方の数)です。この方法表を調べてモデルに含まれていた成分数を判断します。モデル選択プロットを調べることもできます。
PLSを使用する場合、予測変数と応答の変動量が十分なことを説明づける成分数が最小のモデルを選択します。データに最適な成分数を決定するには、X-分散R2が含まれるモデル選択表を調べて、R2の値を予測します。予測R2はモデルの予測能力を示し、交差検証を実行した場合にのみ表示されます。
場合によっては、Minitabによって最初に選択されたモデルとは異なるモデルを使用することもできます。交差検証を使用する場合は、R2と予測R2を比較します。予測R2をわずかしか減少させないモデルから2つの成分を削除した例を検討します。予測R2の減少はわずかであるため、モデルが過剰に適合することはなく、モデルはデータにより良好に適合すると判断できます。
R2よりも大幅に低い予測R2は、モデルの過剰適合を示している可能性があります。過剰適合は、サンプルデータでは重要に見えても母集団には重要でない項や成分を追加した場合に起こります。そのモデルはサンプルデータに即してしまい、母集団の予測に適さなくなる可能性があります。
交差検証を使用しない場合、モデル選択表のX-分散値を調べ、モデルごとに応答の分散がどの程度説明されるかを判断します。
方法
| 交差検証 | 観測値を1つずつ省略 |
|---|---|
| 評価する成分 | 設定 |
| 評価された成分数 | 10 |
| 選択された成分数 | 4 |
方法
| 交差検証 | なし |
|---|---|
| 計算する成分 | 設定 |
| 計算された成分数 | 10 |
主要な結果: 成分数
これらの結果では、1番目の方法表では、交差検証が使用されて、4つの成分を持つモデルが選択されています。2番目の方法表では、交差検証は使用されていません。デフォルトでは、10つの成分を持つモデルを使用されます。
芳香に対するモデル選択および検証
| 成分 | X分散 | 誤差 | R二乗 | 予測残差平方和 (PRESS) | R二乗 (予測) |
|---|---|---|---|---|---|
| 1 | 0.158849 | 14.9389 | 0.637435 | 23.3439 | 0.433444 |
| 2 | 0.442267 | 12.2966 | 0.701564 | 21.0936 | 0.488060 |
| 3 | 0.522977 | 7.9761 | 0.806420 | 19.6136 | 0.523978 |
| 4 | 0.594546 | 6.6519 | 0.838559 | 18.1683 | 0.559056 |
| 5 | 5.8530 | 0.857948 | 19.2675 | 0.532379 | |
| 6 | 5.0123 | 0.878352 | 22.3739 | 0.456988 | |
| 7 | 4.3109 | 0.895374 | 24.0041 | 0.417421 | |
| 8 | 4.0866 | 0.900818 | 24.7736 | 0.398747 | |
| 9 | 3.5886 | 0.912904 | 24.9090 | 0.395460 | |
| 10 | 3.2750 | 0.920516 | 24.8293 | 0.397395 |
主要な結果: X-分散、R二乗、R二乗(予測)
これらの結果では、予測R2の値が約56%となる4つの成分を持つモデルが選択されました。X-分散に基づいて、4つの成分モデルは、予測変数の約60%の分散を説明します。成分数が増えるにつれて、R2の値が上昇しますが、予測R2は減少し、より多くの成分を持つモデルの適合値が過剰になる可能性があることを示しています。
ステップ2: データに外れ値またはてこ比点が含まれているかどうかを判断する
モデルがデータに十分に適合しているかどうかを判断するためには、プロットを調べて、外れ値、てこ比点、および他のパターンを確認する必要があります。データに外れ値またはてこ比点が数多く含まれている場合、モデルは妥当な予測ができない可能性があります。
- 外れ値: 大きな標準化残差を持つ観測値は、プロットの水平方向の参照ラインの外側にあります。
- てこ比点: てこ比の値を持つ観測値は、X―スコアがゼロから離れているので、垂直方向の参照線の右側にあります。
残差対てこ比プロットの詳細は偏最小二乗回帰のグラフを参照してください。
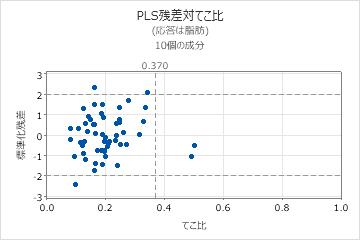
- 点と点の間の非線形パターン。これは、モデルがデータに十分に適合または予測しないことを示します。
- 公差検証を実行した場合、適合値と交差検証された値との間に大きな差が発生し、それがこ比を示します。
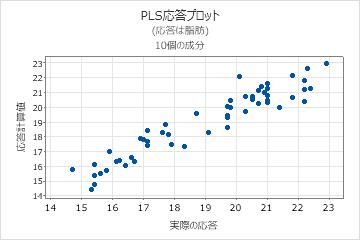
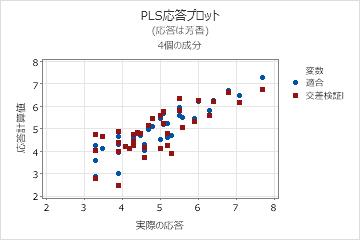
ステップ3. 検定データセットを持つPLSモデルを検証する
しばしば、PLS回帰は2つステップで行われます。最初のステップは、トレーニングと呼ばれることもあり、サンプルデータセット(トレーニングデータセットとも呼ばれる)のPLS回帰モデルを計算します。2番目のステップでは、別のデータセット(検定データセットとも呼ばれる)でこのモデルの検証が行われます。検定データセットでモデルを検証するには、予測サブダイアログボックス上の検定データ列を入力します。Minitabでは、検定データセット内の各観測値について新しい応答値が計算され、予測された応答と実際の応答が比較されます。この比較により、検証R2が計算されます。このことは、モデルに新しい応答を予測する能力があることを示してます。検定R2の値が大きいほど、モデルの予測能力が向上することを示しています。
交差検証を使用する場合は、テストR2を予測R2と比較します。理想的には、両方の値は同様である必要があります。テストR2が予測R2より有意に小さい場合は、交差検証がモデルの予測能力について楽観的過ぎるか、2つのサンプルがそれぞれ異なる母集団のものであることを示しています。
検定データセットに応答値が含まれていない場合、検定R2は計算されません。
脂肪に対するモデルを使用する新しい観測値に対する予測応答
| 行 | 適合値 | 適合値の標準誤差 | 95%信頼区間 | 95%予測区間 |
|---|---|---|---|---|
| 1 | 18.7372 | 0.378459 | (17.9740, 19.5004) | (16.8612, 20.6132) |
| 2 | 15.3782 | 0.362762 | (14.6466, 16.1098) | (13.5149, 17.2415) |
| 3 | 20.7838 | 0.491134 | (19.7933, 21.7743) | (18.8044, 22.7632) |
| 4 | 14.3684 | 0.544761 | (13.2698, 15.4670) | (12.3328, 16.4040) |
| 5 | 16.6016 | 0.348485 | (15.8988, 17.3044) | (14.7494, 18.4538) |
| 6 | 20.7471 | 0.472648 | (19.7939, 21.7003) | (18.7861, 22.7080) |
主要な結果: 検定R2
これらの結果では、検定R2はおよそ76%になります。元のデータセットの予測R2はおよそ78%です。これらの値が近似するので、モデルには十分な予測能力があると結論できます。
