偏最小二乗回帰のモデル選択および検証表

成分は、モデルごとに含まれる成分数を表します。Minitabでは、指定した成分数が含まれるまで、1つの成分を持つモデル、2つの成分を持つモデルといった具合に表示されます。Minitabでは、モデルに含まれる成分数を指定しなかった場合、10個の成分に対するモデル選択統計量と予測変数の内、いずれか少ない方の数が表示されます。

X-分散は、モデルによって説明される項における予測変数の分散量です。X-分散は0～1の値です。

X-分散の値が1に近いほど、成分は元の項を良好に表します。複数の応答がある場合、X-分散値はすべての応答で同じです。

誤差は誤差の平方和であり、残差を二乗した和です。モデルで説明づけられないデータの変動を定量化します。最後のモデルの場合、誤差は、最後のモデル用の分散分析表の残差誤差の平方和と一致します。

R²は、モデルによって説明される応答の変動の割合です。これは、1から合計の平方和 (モデルの全変動) に対する誤差の平方和 (モデルでは説明されない変動) の比率を引いたものとして計算されます。

解釈

R²を使用して、モデルがデータにどの程度適合するかを判断します。R²値が高いほど、データにモデルがより良く適合します。R²は常に0%から100%の間です。

適合線プロットを使用して、さまざまなR²値をグラフィカルに説明することができます。最初のプロットは、応答の変動の85.5%を説明する単回帰モデルを示しています。2番目のプロットは、応答の変動の22.6%を説明するモデルを示しています。モデルによって説明される変動が多いほど、データ点が適合回帰直線に近づきます。理論上、モデルが変動の100%を説明できる場合、適合値は常に観測値と等しく、すべてのデータ点が適合線上に収まります。ただし、R²が100%であっても、そのモデルが必ずしも新しい観測値を良好に予測するとは限りません。

R²値を解釈する際には、次の点を考慮してください。

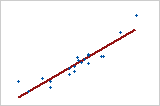
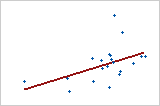
• モデルに他の予測変数を追加すると、R²は常に増加します。たとえば、最良の5つの予測変数のモデルは、常に、低くとも、4つの予測変数のモデルと同じ高さのR²を有します。したがって、R²は、同じサイズのモデルを比較する場合にとても有用です。

• 小さなサンプルでは、応答変数と予測変数の関係の強さの正確な推定値は提供されません。たとえば、より正確にするためにR²が必要な場合は、より大きなサンプル（通常は40以上）を使用する必要があります。

• 適合度の統計量は、モデルがデータにどの程度適合するかの1つの尺度に過ぎません。モデルに望ましい値がある場合でも、残差プロットを確認して、モデルがモデルの前提を満たしていることを検証する必要があります。

予測R²は、計算されたモデルのそれぞれがどの程度応答を予測できるかを示し、交差検証を使用した場合にのみ計算されます。データ内に応答変数が1つある場合、予測R²が最大のPLSモデルが選択されます。複数の応答変数がデータにある場合は、すべての応答変数に対して平均予測R²が最大になるPLSモデルが選択されます。予測R²は、データセットからの各観測値の系統的な削除、回帰式の推定、削除した観測値をモデルがどの程度良好に予測するかの判断によって求められます。予測R²は0%～100%の間の値です（予測されたR²値に負値が算出される場合がありますが、Minitabでは0を表示します）。

予測残差平方和（PRESS）とは、適合値と観測値の偏差を表す測度です。PRESSは二乗残差の和である残差平方和（SSE）と似ています。ただし、PRESSの残差計算方法は異なります。PRESSの計算式は、データセットからの各観測値の系統的な削除、回帰式の推定、削除した観測値をモデルがどの程度良好に予測するかの判断に使われるのと同じです。