このトピックの内容
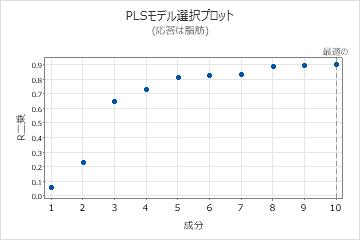
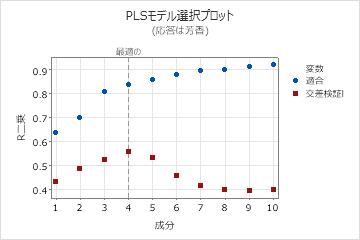
モデル選択プロット
モデル選択プロットは、R2と予測R2の値を、適合または交差検証対象の成分数の関数として示す散布図です。これは、モデル選択および検証表を図で示したものです。交差検証性を使用しない場合は、予測R2の値はプロットに表示されません。Minitabでは、各応答に対してモデル選択プロットが1つ示されます。
解釈
このプロットでは、各モデルのモデリング能力と予測能力を比較して、モデルに含める適切な成分数を決定します。プロット上の縦軸は、PLSモデル用に選択された成分の数を示します。
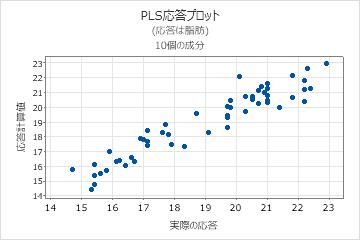
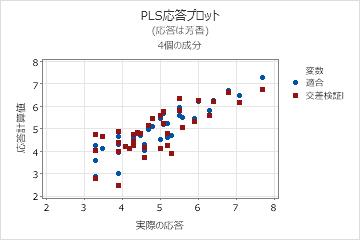
応答プロット
応答プロットは、適合値と実際の応答の散布図です。交差検証性を実行する場合、適合値と交差検証された適合値はプロットに表示されます。Minitabでは、各応答に対して応答プロットが1つ示されます。
解釈
- 点と点の間の非線形パターン。これは、モデルがデータに良好に適合しない、またはデータを良好に予測しないことを示します。
- 公差検証を実行した場合、適合値と交差検証された値との間に大きな差が発生し、それがこ比を示します。
予測能力が優れたモデルでは、通常傾きは1になり、Y軸とは0で交差します。
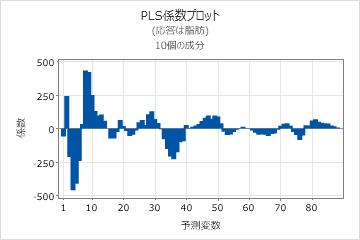
係数プロット
係数プロットは、各予測変数の非標準化係数を示す投影散布図です。Minitabでは、各応答に対して係数プロットが1つ示されます。
解釈
係数プロットと回帰係数の出力を使用して、各予測変数の係数の符号と大きさを比較します。このプロットでは、モデル内である程度重要な予測変数を簡単に識別できます。
このプロットには非標準化係数が表示されるため、予測変数が同じスケール(スペクトルデータなど)である場合は、予測変数と応答との関連の度合いの比較のみを行うことができます。予測変数のスケールが異なる場合は、標準化係数プロットまたは負荷量プロットを使用して、成分の計算に使用される予測変数の重みを比較します。
標準係数プロット
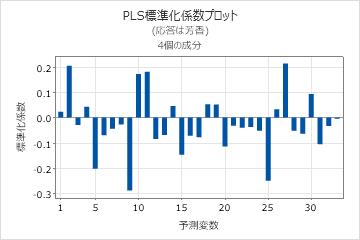
係数プロットは、各予測変数の標準化係数を示す投影散布図です。Minitabでは、各応答に対して標準化係数プロットが1つ示されます。
解釈
このプロットと回帰係数の出力を使用して、各予測変数の係数の符号と大きさを比較します。このプロットでは、モデル内である程度重要な予測変数を簡単に識別できます。
このプロットには標準化係数が表示されるため、予測変数が同じスケールでない場合でも、予測変数と応答との関連の度合いを比較できます。
予測変数が同じスケールの場合、標準化係数プロットと非標準化係数プロットのパターンは類似します。ただし、予測変数の大きな相関によって係数が不安定になること、およびサンプルの標準偏差と母集団の標準偏差との差に起因して、これらのプロットは一致しない場合もあります。
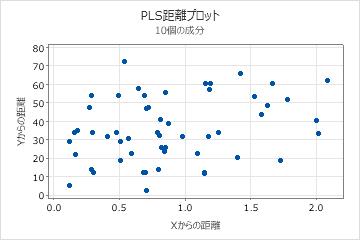
距離プロット
距離プロットは、各観測値のX-モデルおよびX-モデルからの距離の散布図です。Y-モデルからの距離は、観測値がどの程度Y-空間にあてはまるかを示します。X-モデルからの距離は、観測値がどの程度X-空間にあてはまるかを示します。
解釈
このプロットでは、x軸またはy軸で他より大きな距離を持つデータ点を探します。yモデルからの距離がより大きな観測値は、外れ値である可能性があり、xモデルからの距離がより大きな観測値は、てこ比点である可能性があります。
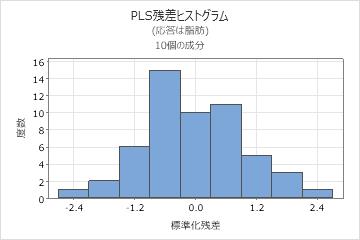
残差のヒストグラム
標準化残差のヒストグラムは、すべての観測値について標準化残差の分布を示します。
解釈
| パターン | パターンが示す意味 |
|---|---|
| 1つの方向に伸びている | 歪度 |
| 1本のバーが他のバーから離れている | 外れ値 |
ヒストグラムの外観は、データをグループ化するために使用されている区間の数に依存するので、残差の正規性を評価するときにヒストグラムは使用しません。その代わり、正規確率プロットを使用します。ヒストグラムは、データ点が約20個以上ある場合に最も効果的です。サンプルが小さすぎる場合、ヒストグラム上の各バーには歪度や外れ値を確実に表示するだけの十分なデータ点がありません。
残差の正規確率プロット
残差の正規確率プロットには、分布が正規分布する場合の標準化残差対期待値の関係が表示されます。
解釈
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
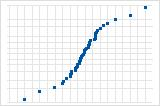
S曲線は、長い裾を持つ分布を示唆しています。
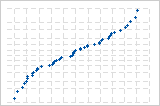
逆S曲線は、短い裾を持つ分布を示唆しています。
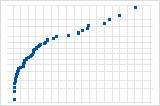
下向きの曲線は、右方向の歪みを示唆しています。
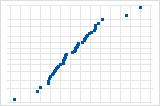
直線から離れている少数の点は、外れ値のある分布を示唆しています。
非正規パターンでは、残差プロットを使用して項抜けや時間順位効果など、モデルの他の問題を確認します。残差が正規分布に従っていない場合、信頼区間とp値は不正確である可能性があります。
残差対適合値
残差対適合値グラフでは、y軸に標準化残差が、x軸に適合値がプロットされます。
解釈
残差対適合値プロットを使用して、残差はランダムに分布し、均一な分散が存在するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |

外れ値のあるプロット
ある点が他の点に比べて大きいため、この点は外れ値となります。外れ値が多すぎる場合は、モデルが適切ではない可能性があります。外れ値の原因を識別する必要があります。データ入力や測定の誤差はすべて修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
不均一分散のプロット
残差の分散が適合値の増加とともに増加しています。適合値が大きくなるにつれ、残差間でばらつきが大きくなっていることに注意してください。このパターンは、残差の分散が等しくない(不均一である)ことを示しています。
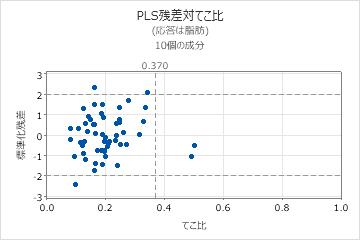
残差対てこ比プロット
残差対てこ比プロットは、各観測値の標準化残差とてこ比を対比させた散布図です。
解釈
- 外れ値:標準化残差の差が±2より大きな観測値。これは、プロットの水平方向の参照ラインの外側にあります。
- てこ比点:てこ比が2m / nより大きな観測値(mは成分数、nは観測値数)。これは過度なてこ比と見なされます。このような観測値はxスコアがゼロから離れており、x軸の2m / n値にある縦の参照ラインより右側にあります。てこ比の値は常に0~1の間にあるため、2m / nの値が1より大きい場合は、プロットに参照ラインは表示されません。
残差対データ順序
残差対順序プロットには、データの収集順に標準化残差が表示されます。
解釈
トレンド
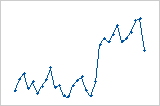
シフト
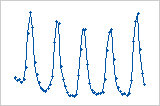
周期
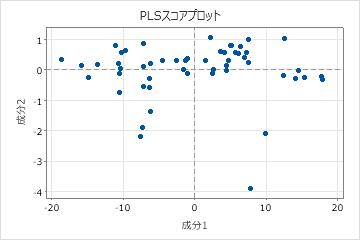
スコアプロット
スコアプロットは、モデルの第1成分と第2成分のX-スコアの散布図です。
解釈
最初の2つの成分が予測変数のほとんどの分散を説明する場合、このプロットのデータ点の配置は、データの元の多次元配置を適切に反映します。モデルによって予測変数の分散がどの程度説明されるかを確認するには、モデル選択および検証表でX分散の値を調べます。X-分散の値が高い場合、モデルは予測変数の有意な分散を示します。
- てこ比点: プロット上でほとんどの点から離れて位置する点は、てこ比点である可能性があり、結果に大きく影響すると考えられます。
- クラスタ: グループ化された点は、データに2つ以上の異なる分布があることを示している可能性があり、他のモデルを使用した方が良好に記述できる場合もあります。
注
モデルに3つ以上の成分が含まれている場合は、散布図を使用して他の成分のX-スコアをプロットできます。これを行うには、X-スコア行列を保存し、を使用して行列をコピーします。モデルに成分が1つしか含まれていない場合、このプロットは出力に表示されません。
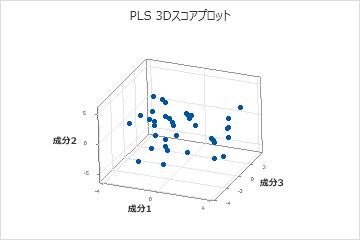
3Dスコアプロット
3Dスコアプロットは、モデルに含まれる第1、第2、および第3成分からのX-スコアの3次元散布図です。最初の3つの成分が予測変数のほとんどの分散を説明する場合、このプロットのデータ点の配置は、データの元の多次元配置を適切に反映します。モデルによって分散がどの程度説明されるかを確認するには、モデル選択および検証表でX-分散の値を調べます。X-分散の値が高い場合、モデルは予測変数の有意な分散を示します。
解釈
- てこ比点: プロット上でほとんどの点から離れて位置する点は、てこ比点である可能性があり、結果に大きく影響すると考えられます。
- クラスタ: グループ化された点は、データに2つ以上の異なる分布があることを示している可能性があり、他のモデルを使用した方が良好に記述できる場合もあります。
また、3Dグラフツールを使用する必要もあります。このツールを使用すると、プロットを回転して別の視点から表示できます。これにより、データを詳しく考察することができ、てこ比点と点のクラスタをより正確に識別できます。
負荷量プロット
負荷量プロットは、モデルの第1および第2成分上に投影された予測変数の散布図です。第1成分のX負荷量に対して第2成分のX負荷量がプロットされます。予測変数を表す個々の点は、プロットの(0,0)につながります。
解釈
負荷量プロットは、予測変数が最初の2つの成分においてどの程度重要であるかを示し、予測変数が異なるスケールの場合は特に便利です。これらの成分がモデル選択および検証表のX分散のほとんどを説明する場合、負荷量プロットはX-空間における予測変数の重要度を示します。モデル全体での予測変数の重要度を考慮する場合は、成分が応答における分散をどの程度説明するかも考慮する必要があります。これを確認するには、モデル選択および検証表でR2と予測R2の値を調べます。
- 直線間の角度。この角度は予測変数間の相関を表します。角度が小さい場合、予測変数の相関が高いことを示しています。
- より長い直線を持つ予測変数。これは第1または第2成分でより大きな負荷量を持ち、モデル内でより重要です。

注
モデルに3つ以上の成分が含まれている場合は、散布図を使用して他の成分のX-負荷量をプロットできます。これを行うには、X-負荷量行列を保存し、を使用して行列をコピーします。
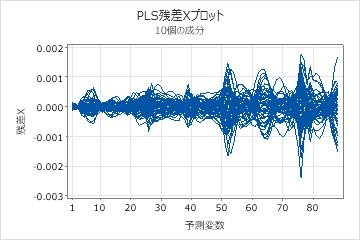
残差Xプロット
残差XプロットはX-残差対予測変数のラインプロットです。各ラインは観測値を表し、その観測値が持つ予測変数と同じ数の点を持ちます。
解釈
X-残差行列プロットを使用すると、モデルで十分に記述されない観測値または予測変数を識別できます。このプロットは、同じスケールの予測変数で使用する場合に最も便利です。
- X軸の同じ点においてラインの間隔が広い場合、モデルはその点における予測変数を十分に記述しません。
- ラインが他のラインから逸脱している場合、モデルはそのラインで表される観測値を十分に記述しません。
X-残差行列プロットを使用して、残差の一般的なパターンを確認し、問題がある領域を識別します。次に、出力に表示されたX-残差を調べて、モデルで十分に記述されない観測値と予測変数を判断します。
X-計算値のプロット
Xー計算値のプロットはX-計算値対予測変数のラインプロットです。各ラインは観測値を表し、その観測値が持つ予測変数と同じ数の点を持ちます。
解釈
このプロットを使用すると、モデルで十分に記述されない観測値または予測変数を識別できます。このプロットは、同じスケールの予測変数で使用する場合に最も便利です。
Xー計算値のプロットはX-残差プロットを補います。両方のプロットの和は、元の予測変数値のプロットになります。元のX-値より非常に小さな、または非常に大きなX-計算値を持つ予測変数は、モデルによって適切に記述されません。

