適合値
適合した値は、適合値またはとも呼ばれます。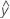
適合した値は、予測変数の任意の値に対する平均応答の点推定です。予測変数の値は、Ｘ-値とも呼ばれます。
解釈
適合値は、データセットに含まれる観測値ごとの特定のx値をモデル式に入力することによって計算されます。
たとえば、式がy = 5 + 10xの場合に、X-値が2ならば、適合値は25（25 = 5 + 10(2)）となります。
残差（Res）
残差（ei）とは、観測値（y）とそれに対応する適合値（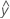
）の差であり、モデルによって予測される値です。
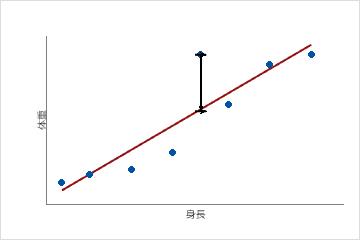
この散布図は、成人男性の体重対身長を表示します。適合回帰線は身長と体重の関係を表します。身長が6フィートの場合、体重の適合値は190ポンドです。実際の体重が200ポンドの場合、残差は10となります。
解釈
残差をプロットすると、モデルが適切であり、回帰仮定が満たされているかどうかを確認できます。残差を調べることにより、データに対するモデルの適合度に関して有用な情報を得ることができます。一般的に、残差はランダムに分布し、明確なパターンや異常値がありません。
標準化残差（SRes）
標準化残差は、残差（ei）をその標準偏差の推定値で割ったものです。
解釈
標準化残差を使用すると、外れ値を検出しやすくなります。
生データの残差は外れ値の指標としては適さないため、標準化残差が役に立ちます。生データの各残差の分散は、その残差に関連するX-値によって異なります。この尺度が等しくないため、生データの残差のサイズを評価するのは困難です。さまざまな分散をよく使用される尺度に置き換えて、この残差を標準化することにより、問題は解決されます。
交差検証された適合値
PLS回帰の場合、交差検証された適合値は、個別に計算されるデータセット内の各観測値の予測応答であるため、観測値の予測応答の計算に使用されるモデルからその観測値を除外することができます。交差検証された適合値は、交差検証の過程で計算され、除外される観測値の数に応じてモデルが再計算されるたびに異なります。
交差検証された適合値を使用して、モデルがどの程度データを予測するかを特定します。交差検証された適合値は、モデルのデータへの適合度を特定する通常の適合値と同様です。
交差検証された残差
PLS回帰の場合、交差検証された残差は、実際の応答と交差検証された適合値との差です。交差検証された残差値は、交差検証の過程でモデルが再計算されるたびに除外される観測値の数に応じて異なります。
この残差はモデルの予測能力を測定します。交差検証された残差を使用して、PRESS統計量を計算します。
