目的の方法または計算式を選択してください。
回帰式
測定誤差モデルは以下になります。
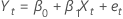
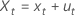
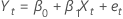
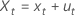
直交回帰では、最も適合する直線は、プロットした点から直線までの重み付きの直交距離が最小になる直線です。誤差分散比が1の場合は、重み付き距離はユークリッド距離です。
表記
| 用語 | 説明 |
|---|---|
| Yt | 観測された応答値 |
| β0 | 切片 |
| β1 | 傾き |
| Xt | 観測された予測変数 |
| xt | 観測されていない本当の予測変数値 |
| et, ut | 測定誤差。et, utは平均0、δe2の誤差分散、およびδu2から独立しています。 |
共分散行列のサンプル
サンプルの平均を（
、
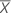）、共分散行列のサンプルを以下にしたとします。
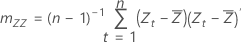
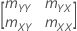
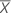、）、共分散行列のサンプルを以下にしたとします。
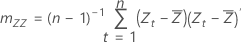
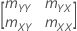
表記
| 用語 | 説明 |
|---|---|
| Zt | (Yt, Xt) |
 |  |
| n | サンプルサイズ |
誤差分散
サンプルの共分散行列は、以下の2 × 2行列です。
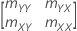
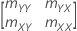
共分散行列サンプルの要素mXYは0ではなく、以下になります。
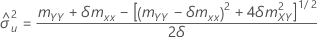
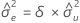
mxy = 0かつmyy < δm xx''の場合、
表記
| 用語 | 説明 |
|---|---|
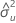 | Xの誤差分散の推定値 |
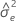 | Xの誤差分散の推定値 |
| δ | 誤差分散比 |
| mXY | 共分散行列サンプルの要素 |
| mYY | 共分散行列サンプルの要素 |
| mXX | 共分散行列サンプルの要素 |
係数
共分散行列サンプルの要素mXYが0でない場合は以下になります。
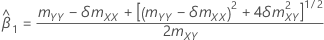
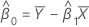
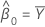
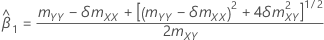
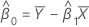
mxy = 0かつmyy < δm xx''の場合、
mxy = 0かつmyy > δmxxの場合、残りのパラメータ推定値は未定義です。
表記
| 用語 | 説明 |
|---|---|
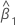 | 傾きの推定値 |
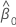 | 切片の推定値 |
| mxy | 共分散行列サンプルの要素 |
| myy | 共分散行列サンプルの要素 |
| δ | 誤差分散比 |
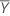 | 応答値の平均 |
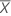 | 予測変数値の平均 |
近似分布の共分散行列
切片と傾きの近似分布の共分散行列の推定値:
ここで、
および
mXY = 0ではない場合、
If mXY = 0かつmYY < δmXXの場合、
表記
| 用語 | 説明 |
|---|---|
 | 傾きの推定値 |
 | 切片の推定値 |
| mXY | 共分散行列サンプルの要素 |
| mYY | 共分散行列サンプルの要素 |
| mXX | 共分散行列サンプルの要素 |
| δ | 誤差分散比 |
 | 応答値の平均 |
 | 予測変数値の平均 |
切片の信頼区間
β0の100(1 - α)%信頼区間は以下になります。
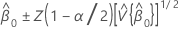
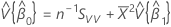近似分布の共分散行列の要素です
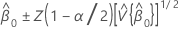
Z(1 - α / 2)は標準正規分布の100 * (1 - α / 2)百分位数
および
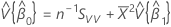近似分布の共分散行列の要素です表記
| 用語 | 説明 |
|---|---|
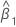 | 傾きの推定値 |
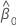 | 切片の推定値 |
| α | 有意水準 |
傾きの信頼区間
β1の100(1 - α)%の信頼区間は以下になります。
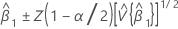
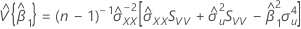
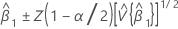
ここで、
Z(1 - α / 2)は標準正規分布の100 * (1 - α / 2)百分位数
および
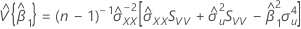
表記
| 用語 | 説明 |
|---|---|
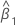 | 傾きの推定値 |
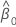 | 切片の推定値 |
| α | 有意水準 |
ｘの適合値
直交回帰での予測変数xの適合値は以下になります。
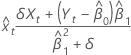
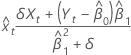
表記
| 用語 | 説明 |
|---|---|
| δ | 誤差分散比 |
| Yt | t番目の応答値 |
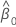 | 切片の推定値 |
 | 傾きの推定値 |
yの適合値
直交回帰での応答yの適合値は以下になります。
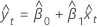
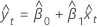
表記
| 用語 | 説明 |
|---|---|
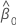 | 切片の推定値 |
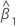 | 傾きの推定値 |
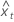 | xのt番目の適合値 |
残差
直交回帰での観測値の残差は以下になります。
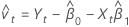
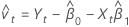
表記
| 用語 | 説明 |
|---|---|
| Yt | t番目の応答値 |
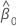 | 切片 |
| Xt | t番目の予測変数値 |
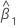 | 傾き |
標準化残差
標準化残差は外れ値の特定に役立ちます。以下のように計算されます。
ここで
表記
| 用語 | 説明 |
|---|---|
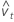 | 残差 |
 | 残差の標準偏差 |
| δ | 誤差分散比 |
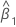 | 傾きの推定値 |
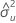 | Xの誤差分散の推定値 |
Yの予測変数
Yn + 1の予測変数は以下になります。
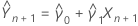
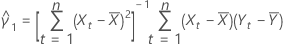
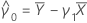
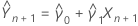
ここで、
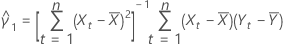
および
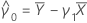
表記
| 用語 | 説明 |
|---|---|
| Xt | t番目の予測変数値 |
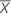 | 予測変数値の平均 |
| Yt | t番目の応答値 |
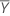 | 応答値の平均 |
予測誤差の標準偏差
ここで、
表記
| 用語 | 説明 |
|---|---|
| myy | Yのサンプル分散 |
| mxy | XとYの確率変数間のサンプル共分散 |
