直交回帰分析を解釈するには、次の手順を実行します。主要な出力値には、係数の信頼区間、適合線プロット、残差プロットが含まれています。
ステップ1: 2つの計器または方法の測定値が異なるかどうかを判断します
臨床化学や試験室などでは、2つの機器や手法から同等な測定値を得られるかどうかを判断するのに、よく直行回帰が使われます。定数項の信頼区間に0が含まれており、線形項の区間に1が含まれる場合、2つの機器から得られる測定値は同等であると、多くの場合結論付けることができます。
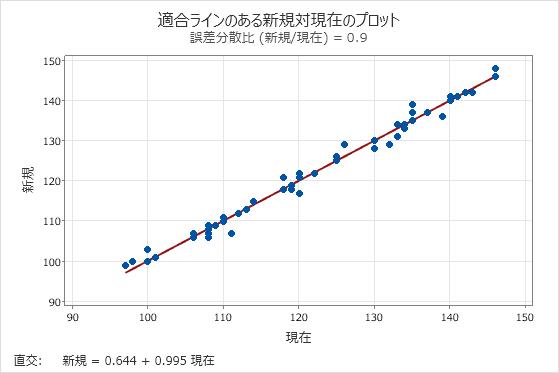
適合線を持つプロットを調べて、モデルがどの程度データに適合するかを判断する必要もあります。
誤差分散比 (新規/現在): 0.9
回帰式
新規 = 0.644 + 0.995 現在
新規 = 0.644 + 0.995 現在
係数
| 予測変数 | 係数 | 係数の標準誤差 | z値 | p値 | 近似95%信頼区間 |
|---|---|---|---|---|---|
| 定数 | 0.64441 | 1.74470 | 0.3694 | 0.712 | (-2.77513, 4.06395) |
| 現在 | 0.99542 | 0.01415 | 70.3461 | 0.000 | (0.96769, 1.02315) |
誤差分散
| 変数 | 分散 |
|---|---|
| 新規 | 1.07856 |
| 現在 | 1.19840 |
主要な結果: およそ95%の信頼区間(CI)
これらの結果では、定数項の信頼区間はおよそ(−3,4)になります。信頼区間には0が含まれているので、分析のこの部分は、2つの計器の測定値が異なるという根拠にはなりません。
線形項の信頼区間はおよそ(0.97,1.02)になります。信頼区間には1が含まれているので、分析のこの部分は、2つの計器の測定値が異なるという根拠にはなりません。
いずれの区間も、2つの計器の測定値が異なるという根拠にはならないので、通常は、測定値は比較可能と結論づけます。適合線を持つプロットと残差プロットを調べることによって、モデルがデータに十分に適合することを検証する必要もあります。
ステップ2:回帰線がデータに適合するかどうか判断する
プロットと適合線を使用して、直交回帰式がデータに適合するかどうかを評価します。モデルがデータに適合すると、データ点は回帰線付近に分布します。とりわけ、これらの基準の適合線を調べることができます。
- サンプルには、すべての予測変数値の範囲全体にわたって十分な数の観測値が含まれます。
- サンプルには、モデルが適合しない曲率は含まれません。
- サンプルには、結果に大きな影響を与える可能性のある外れ値は含まれません。外れ値がある場合は、その原因を特定してください。データ入力を修正するか、測定の誤差を識別します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
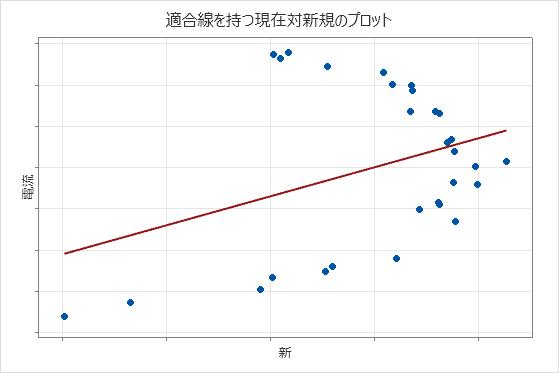
このプロットは、比較可能な2つの計器または方法から測定の例を示しています。このプロットでは、方法間の体系的な差を示すパターンなしで、分散が最小の適合線に従います。
以下の結果では、係数の信頼区間は、2つの計器の測定値が異なるという根拠を示していません。しかし、点が適合線付近に分布していないことは明らかであり、このことは、2つの計器の測定値が比較できないことを示しています。データが式に適合していないため、これらの計器は異なるというのが通常の結論です。
係数
| 予測変数 | 係数 | 係数の標準誤差 | z値 | p値 | 近似95%信頼区間 |
|---|---|---|---|---|---|
| 定数 | -0.00000 | 0.215424 | -0.0000 | 1.000 | (-0.422224, 0.42222) |
| 新規 | 1.00000 | 0.517586 | 1.9320 | 0.053 | (-0.014450, 2.01445) |