適合線を持つプロット
適合線を持つプロットでは、応答と予測変数データを表示します。このプロットには、直行回帰式を表す直行回帰線が含まれます。
比較のために、プロットに通常の最小二乗法適合線を表示することもできます。2本の線の差が大きい場合、予測変数の値に関する不確実性を説明するかどうかに結果が依存する大きさを示します。最小二乗値は直交回帰の予測値と等しいので、最小二乗線を使用して予測値を使用することもできます。
解釈
- サンプルには、すべての予測変数値の範囲全体にわたって十分な数の観測値が含まれます。
- サンプルには、モデルが適合しない曲率は含まれません。
- サンプルには、結果に大きな影響を与える可能性のある外れ値は含まれません。外れ値がある場合は、その原因を特定してください。データ入力を修正するか、測定の誤差を識別します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
臨床化学や実験で直交回帰を使用して、2つの計器または方法が比較可能な測定になるかどうかを判断することがよくあります。
このプロットは、比較可能な2つの計器または方法から測定の例を示しています。このプロットでは、方法間の体系的な差を示すパターンなしで、分散が最小の適合線に従います。
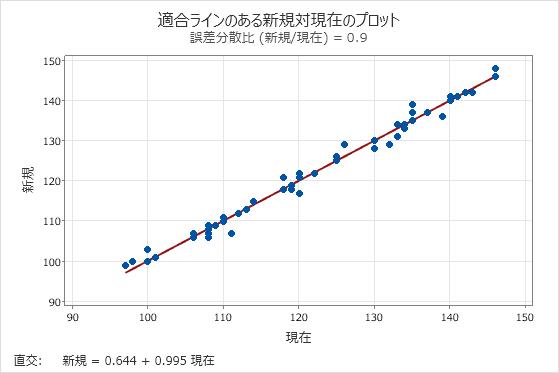
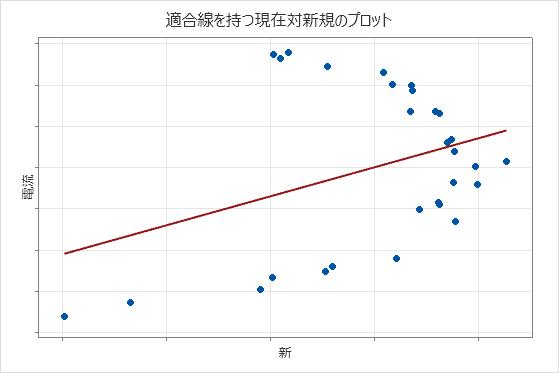
以下の結果では、係数の信頼区間は、2つの計器の測定値が異なるという根拠を示していません。しかし、点が適合線付近に分布していないことは明らかであり、このことは、2つの計器の測定値が比較できないことを示しています。データが式に適合していないため、これらの計器は異なるというのが通常の結論です。
係数
| 予測変数 | 係数 | 係数の標準誤差 | z値 | p値 | 近似95%信頼区間 |
|---|---|---|---|---|---|
| 定数 | -0.00000 | 0.215424 | -0.0000 | 1.000 | (-0.422224, 0.42222) |
| 新規 | 1.00000 | 0.517586 | 1.9320 | 0.053 | (-0.014450, 2.01445) |
残差のヒストグラム
残差のヒストグラムは、すべての観測値について残差の分布を示します。
解釈
| パターン | パターンが示す意味 |
|---|---|
| 一方向に伸びている | 歪度 |
| 1本のバーが他のバーから離れている | 外れ値 |
臨床化学または実験で直交回帰を使用して、2つの計器または方法が同じものを測定するかを判断することがよくあります。モデルが仮説を満たさない場合、これらの方法が同じものを測定できないと説明づけることもできます。
ヒストグラムの外観は、データをグループ化するために使用する区間の数によって変わるので、残差の正規性を評価するためにはヒストグラムを使用しません。その代わり正規確率プロットを使用します。
ヒストグラムは、データ点が約20個以上ある場合に最も効果的です。サンプルが小さすぎる場合、ヒストグラムの各バーには、歪度または外れ値が高い信頼性を示すほど十分なデータ点は含まれません。
残差の正規確率プロット
残差の正規確率プロットには、分布が正規分布する場合の残差と期待値の関係が表示されます。
解釈
残差の正規確率プロットを使用して、残差が正規分布に従うという仮定を検証します。残差の正規確率プロットは、ほぼ直線になります。
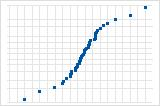
S曲線は、長い裾を持つ分布を示唆しています。
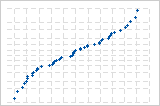
逆S曲線は、短い裾を持つ分布を示唆しています。
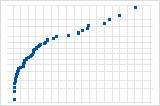
下向きの曲線は、右方向の歪みを示唆しています。
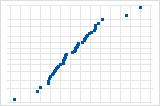
直線から離れている少数の点は、外れ値のある分布を示唆しています。
臨床化学または実験で直交回帰を使用して、2つの計器または方法が同じものを測定するかどうかを判断することがよくあります。非正規パターンを確認する場合、これらの方法が測定するものが同じではないと説明づけることもできます。また、時間順序効果などのモデルの他の問題がないか、他の残差プロットを調査します。残差が正規分布に基づかない場合、信頼区間とp値が不正確である可能性があります。
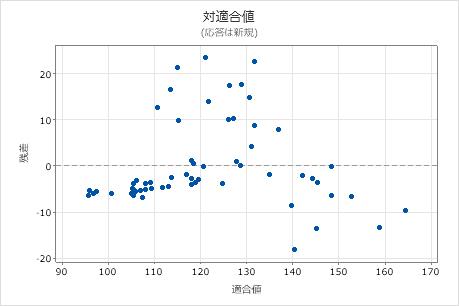
残差対適合値
残差対適合値グラフでは、y軸に残差が、x軸に予測変数の適合値がプロットされます。
臨床化学または実験で直交回帰を使用して、2つの計器または方法が同じものを測定するかどうかを判断することがよくあります。モデルが仮説を満たさない場合、これらの方法が測定するものが同じではないと説明づけることもできます。
解釈
残差対適合値プロットを使用して、残差はランダムに分布し、均一な分散が存在するという仮定を検証します。点に特徴的なパターンがなく、0の両側にランダムにくるのが理想的です。
| パターン | パターンが示す意味 |
|---|---|
| 残差が適合値周辺に扇状または不均等に分散している | 不均一分散 |
| 曲線 | 高次の項の欠損 |
| ゼロから遠い点 | 外れ値 |
| ある点が他の点からX軸方向に遠く離れている | 影響力のある点 |

外れ値のあるプロット
ある点が他の点に比べて大きいため、この点は外れ値となります。外れ値が多すぎる場合は、モデルが適切ではない可能性があります。外れ値の原因を識別する必要があります。データ入力や測定の誤差はすべて修正します。異常な1回だけの事象(特殊原因)に関連付けられたデータ値を除外することを検討してください。それから、分析を繰り返します。
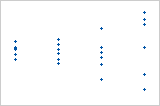
不均一分散のプロット
残差の分散が適合値の増加とともに増加しています。適合値が大きくなるにつれ、残差間でばらつきが大きくなっていることに注意してください。このパターンは、残差の分散が等しくない(不均一である)ことを示しています。
残差対データ順序
残差対データ順序プロットには、データの収集順に残差が表示されます。
解釈
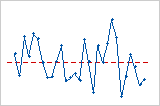
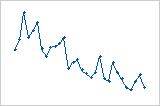
トレンド
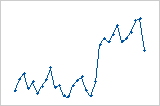
シフト
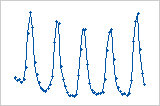
周期
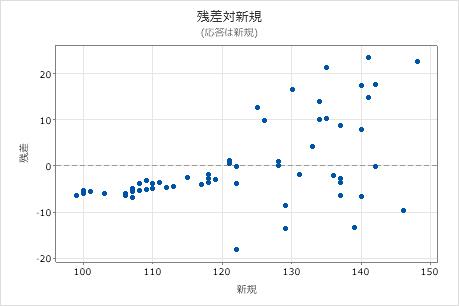
残差対変数
残差対変数プロットには、別の変数に対する残差の値が表示されます。変数はモデルに取り込むことができるようになりました。あるいは、変数はモデルにないかもしれませんが、応答に影響を与えると考えられます。
解釈
臨床化学または実験で直交回帰を使用して、2つの計器または方法が同じものを測定できるかを判断することがよくあります。応答変数または予測変数に対する残差プロットのパターンは、1つの方法が別の方法とどのように異なるかを明確にできます。
これらの結果では、残差対適合プロットは、すべての高い値の残差がプロットの真ん中にあるパターンを表示します。残差対応答変数のプロットにより、新しい方法の読み取り値が大きくなるにつれて、他の方法との整合性は低くなることが明らかになります。