医療機器会社のあるエンジニアは、自社の新しい血圧計が他社の類似する血圧計と等価であるかどうかを調べようとしています。エンジニアは、両方の血圧計を使用して60人のランダムサンプルの最高血圧を測定します。
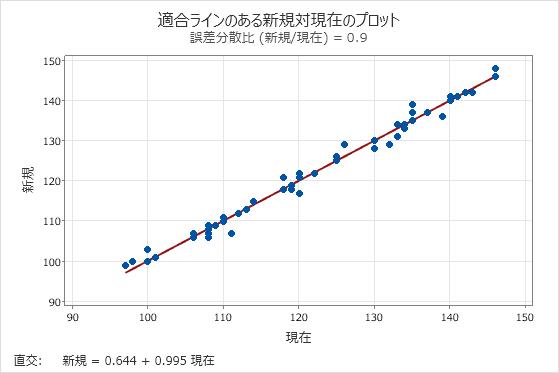
2つの血圧計が等価であるかどうかを判断するため、エンジニアは直交回帰を使用します。直交回帰用にデータを収集する前に、各血圧計について測定を行い、分散を推定します。新しい血圧計の分散は1.08でした。他社の血圧計の分散は1.2でした。新しい血圧計を応答変数とし、他社の血圧計を予測変数に割り当てます。この割り当てでは、誤差分散率は1.08 / 1.2 = 0.9です。
注
この割り当てを反対にする場合、誤差分散率は1.2 / 1.08 = 1.1111です。
- 標本データを開く、 血圧.MWX.
- を選択します。
- 応答 (Y)に新規を入力します。
- 予測変数 (X)に現在を入力します。
- 誤差分散比 (Y/X)に、「0.90」と入力します。
- OKをクリックします。
結果を解釈する
以下の条件のいずれかが真の場合、結果は、血圧計の値が等しくないという根拠にはなりません。
- 傾きの信頼区間に1は含まれません。
- 定数の信頼区間に0は含まれません。
誤差分散比 (新規/現在): 0.9
回帰式
新規 = 0.644 + 0.995 現在
新規 = 0.644 + 0.995 現在
係数
| 予測変数 | 係数 | 係数の標準誤差 | z値 | p値 | 近似95%信頼区間 |
|---|---|---|---|---|---|
| 定数 | 0.64441 | 1.74470 | 0.3694 | 0.712 | (-2.77513, 4.06395) |
| 現在 | 0.99542 | 0.01415 | 70.3461 | 0.000 | (0.96769, 1.02315) |
誤差分散
| 変数 | 分散 |
|---|---|
| 新規 | 1.07856 |
| 現在 | 1.19840 |